DEMOSTRACIONES DE LAS FÓRMULAS
DEL TÉRMINO GENERAL Y DE LA SUMA DE LOS TÉRMINOS EN UNA PROGRESIÓN ARITMÉTICA
La fórmula del término general o del término enésimo de una progresión aritmética depende de la diferencia en común y del primer término de la sucesión. Vamos a demostrar la fórmula por inducción.
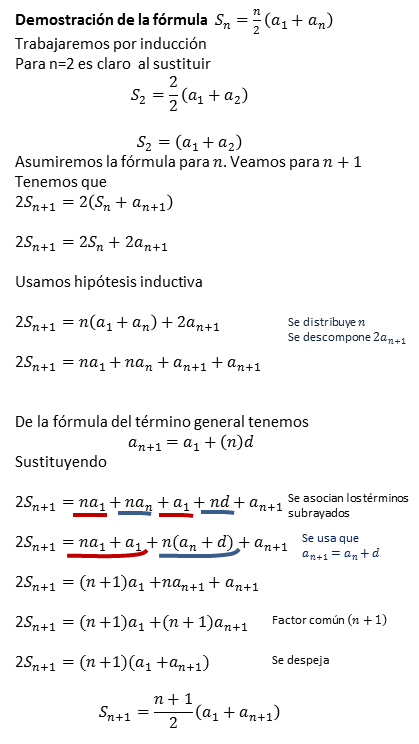
La sumatoria de los primeros términos de una progresión aritmética
puede ser calculada rápidamente usando la fórmula que depende sólo del primer y último término. Mostramos dos pruebas.
Podemos caracterizar el término general de una progresión aritmética a partir del último término. Interpretando los términos de la sucesión en sentido inverso, entonces se tendría una sucesión aritmética con primer término y diferencia en común $d$. No es dificil entonces intuir la siguiente fórmula.
Una deducción formal se puede hacer usando el principio de inducción, procediendo de manera similar a la de la fórmula del término general. Una prueba distinta es truncando los primeros términos y aplicando la fórmula del término general a la sucesión truncada para luego despejar $a_i$.
La sumatoria de los primeros términos de una progresión aritmética
puede ser calculada rápidamente usando la fórmula que depende sólo del primer y último término. Mostramos dos pruebas.
Fórmula para la suma de los primeros
$n$
términos de una progresión aritmética
Podemos caracterizar el término general de una progresión aritmética a partir del último término. Interpretando los términos de la sucesión en sentido inverso, entonces se tendría una sucesión aritmética con primer término y diferencia en común $d$. No es dificil entonces intuir la siguiente fórmula.
Una deducción formal se puede hacer usando el principio de inducción, procediendo de manera similar a la de la fórmula del término general. Una prueba distinta es truncando los primeros términos y aplicando la fórmula del término general a la sucesión truncada para luego despejar $a_i$.