Inecuaciones o desigualdades en una variable

Video 1
DESIGUALDADES EN UNA VARIABLE

Se define desigualdades en una variable, también conocidas como inecuaciones. Se explica el significado de solución, resolver y conjunto solución de una desigualdad. El concepto de intervalo es introducido mediante desigualdades cuyas soluciones son evidentes. Desigualdades dobles del tipo a < x < b son tratadas como una abreviación de desigualdades simultáneas: a< x y x <b.

Ejercicios para después del video
1) Dada la desigualdad 3x-1>5x-3, diga cuáles de los siguientes números es solución. Justifique en cada caso
1.1) 3; 1.2) –7; 1.3) 10; 1.4) 0
2) Grafique las siguientes desigualdades en la recta real y escriba el conjunto solución en términos de intervalos
   
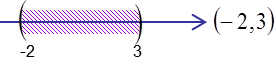
3) Diga, de manera verbal, el conjunto solución de la desigualdad 3>x>-2. Grafique la desigualdad en la recta real y escriba el conjunto solución en la notación de intervalos

Video 2
PROPIEDADES DE DESIGUALDADES I
DESIGUALDADES EQUIVALENTES

Se empieza dando una estrategía general para resolver desigualdades, la cuál usa el concepto de desigualdades equivalentes. La introducción del video pretende motivar el aprendizaje de las propiedades de desigualdades. Se expone la ley aditiva, mostrando ejemplos numéricos en que se visualiza que la ley se cumple. Luego, se muestra cómo esta ley ayuda a resolver inecuaciones. Se justifica cómo la regla es aplicada en la práctica de una manera más versátil, transponiendo términos. Se establece la primera parte de la ley multiplicativa

Ejercicios para después del video
4) Lleve cada desigualdad a otra equivalente en que la solución sea evidente ($x\lt a$, $x\gt a$ ó con desigualdad no estricta), aplicando las propiedades de las desigualdades

Video 3
PROPIEDADES DE DESIGUALDES II
OPERACIONES QUE PRODUCEN DESIGUALDADES EQUIVALENTES

Este video continua con las propiedades de desigualdades, discutiendo la segunda parte de la ley multiplicativa y viendo cómo ella ayuda a resolver desigualdades. Se comentan operaciones que deben ser evitadas al resolver desigualdades. Finalmente se establece una lista de operaciones que producen desigualdades equivalentes.

Ejercicios para después del video
5) Lleve cada desigualdad a otra equivalente en que la solución sea evidente (x < a, x > a ó con desigualdad no estricta).

Cuestionario resumen
1) ¿Qué es una inecuación o desigualdad con una Incógnita?
2) Defina:
   Solución de una desigualdad.
   Conjunto solución
   Resolver una desigualdad
3) ¿Cómo puede verificar si un número es o no solución de una desigualdad?
4) ¿Puede existir desigualdades con infinitas soluciones? ¿con una solución? ¿Sin solución?
5) Diga qué significa la desigualdad doble del tipo $a\lt x\lt b$ . Diga en palabras que representa, qué abrevia.
6) Muestre los tipos de intervalos. Para cada tipo de intervalo indique una desigualdad cuya solución es evidente con conjunto solución el intervalo señalado. Haga la gráfica de cada desigualdad.
7) ¿Qué son desigualdades equivalentes?
8) Explique una estrategía general para resolver desigualdades. 9) Enuncie leyes de las desigualdades que cuando se aplican producen desigualdades equivalentes en que se conserva el sentido de la desigualdad.
10) Enuncie alguna ley de las desigualdades usada para resolver desigualdades que cuando se aplican producen desigualdades equivalentes en que el sentido de la desigualdad se invierte.
11) Explique cómo obtener desigualdades equivalentes.
12) Explique la transposición de términos, es decir cómo proceder si un término que está sumando o restando en una lado de la desigualdad lo queremos pasar al otro miembro. Explique cómo proceder en el caso que esté un número multiplicando o dividiendo.
13) Podemos pasar un factor (que está multiplicando) que contenga la variable dividiendo al otro lado de la desigualdad.

Respuestas