Ecuaciones logarítmicas
con bases distintas

Pueden surgir ecuaciones logarítmicas con varios logaritmos en que las bases difieren. Básicamente para resolver este problema se usa como primer paso la fórmula de cambio de base $$\log_b(x)=\frac{\log_a(x) }{\log_a(b)}$$ Esta fórmula lleva un logaritmo en base $b$ a un logaritmo en base $a$
Mostramos varios ejemplos en que las diferencias estarán en si las bases guardan una relación de potencias exactas una entre otras y si los argumentos son iguales o no.

Argumentos iguales, bases con relación de potencias


Ejemplo
Resolver $2\log_2(x+1)-\log_4(x+1)=1$
Solución

Pulsa el botón para ver el desarrollo del paso.

Vemos que la base 4 es una potencia de la base $2$, esto es $2^2=4$, entonces se lleva el logaritmo de base 4 a base 2.

Se aplica la fórmula de cambio de variable al logaritmo en base 4
Por la fórmula de cambio de base, $ \log_4(x+1) =\frac{ \log_2(x+1) }{\log_2(4) }$
Al sustituir, la ecuación queda
$$2\log_2(x+1)- \frac{ \log_2(x+1) }{\log_2(4) } =1$$

Se simplifica $\log_2(4)$
Como $\log_2(4)=\log_2(2^2)=2$ la ecuación queda
$$2\log_2(x+1)- \frac{ \log_2(x+1) }{2 } =1$$

La ecuación se lleva a la forma un solo logaritmo igual a constante.
Hay que llevarlo a la forma $\log_2(**)=constante$. Primero es conveniente eliminar los denominadores multiplicando ambos lados de la ecuación por dos.
$${\small { 2\cdot \left( 2\log_2(x+1)- \frac{ \log_2(x+1) }{2 } \right) = 2\cdot 1}} $$
$$ {\small {2\cdot \left( 2\log_2(x+1)- \frac{ \log_2(x+1) }{2 } \right) = 2\cdot 1}} $$ Distribuimos y simplificamos $$ 4\log_2(x+1)- \log_2(x+1) =2 $$ Los logaritmos tienen la misma base y argumento. Sacamos $\log_2(x+1)$ de factor común.
$$ \log_2(x+1)(4- 1) =2 $$ $$ \log_2(x+1) \cdot 3 =2 $$ Dividimos por $3$ $$\log_2 {(x+1) } =\frac{2}{3} $$

Se resuelve la ecuación logarítmica resultante
La resolvemos convintiendo la forma logarítmica en forma exponencial, la base es $2$ y el exponente de la forma exponencial es $\frac{2}{3}$ $$ 2 ^\frac{2}{3} =x+1 $$ Quedó una ecuación lineal, despejamos la variable: $$x=\sqrt[3]{4} -1 $$

Eliminar las soluciones que hagan algún argumento no positivo
El único tipo de argumento es $x+1$, al evaluarlo en $x=\sqrt[3]{4} -1$, obtenemos $\sqrt[3]{4}>0$. Por tanto, la solución encontrada $ x=\sqrt[3]{4} -1$ es de la original.

Comentario
 La manera desarrollada ahorra mucho trabajo, sin embargo, no sirve para algunas ecuaciones logaritmicas con distintas bases.

Otra forma de trabajar
En el paso 3 se pudo usar las propiedades de los logaritmos.





   


Argumentos distintos, bases con relación de potencias


Ejemplo Resolver $\log_2(x+1)=\log_4(x+3)$
Solución
Vemos que la base 4 es una potencia de la base $2$, esto es $2^2=4$, entonces se usa un sólo cambio de base.
Se aplica la fórmula de cambio de variable al logaritmo en base 4
Por la fórmula de cambio de base, $ \log_4(x+3) =\frac{ \log_2(x+3) }{\log_2(4) }$ tenemos
$$\log_2(x+1)= \frac{ \log_2(x+3) }{\log_2(4) } $$

Se simplifica $\log_2(4)$
Como $\log_2(4)=\log_2(2^2)=2$ la ecuación queda
$$\log_2(x+1)= \frac{ \log_2(x+3) }{2 } $$

La ecuación se lleva a la forma un logaritmo igual a otro, con las mismas bases.

No está en la forma $\log_2(**)=\log_2(***)$.
Pasamos 2 a multiplicar al lado izquierdo $$2\cdot \log_2(x+1)= \log_2(x+3) $$ Para llevarlo a un logaritmo igual a otro aplicamos la propiedad del logaritmo de una potencia en el lado izquierdo $$ \log_2(x+1)^2 = \log_2(x+3) $$

Se plantea la ecuación un argumento igual al otro. (Como la función logarítmica es biunívoca, dos logaritmos son iguales si sus argumentos son iguales)
$$ (x+1)^2 = x+3 $$

Se resuelve la ecuación resultante
Es cuadrática, se lleva a la forma general $ax^2+bx+c=0$, primero desarrollamos el binomio al cuadrado $$ x^2+2x+1=x+3$$ $$ x^2+x-2=0$$ Podemos resolverla por la fórmula cuadrática, pero más sencillo, factorizando el lado que no es cero. $$(x+2)(x-1)=0$$ Usando la propiedad multiplicativa del cero tenemos $$x+2=0 \qquad o \qquad x-1=0$$ De aquí, las soluciones de la ecuación cuadrática son $-2$ y $1$

Eliminar las soluciones que hagan algún argumento no positivo
La solución $x=-2$ debe ser eliminada, pues en este caso, el argumento $x+1$ es negativo para este valor. La otra solución de la ecuación cuadrática, $x=1$, si es solución de la ecuación logarítmica, pues ambos argumentos son positivos para este valor.
En definitiva, la ecuación logarítmica dada tiene una sola solución, $x=1$





Veamos otra ecuación con un logaritmo neperiano y otro decimal, con los mismos argumentos. Podemos o bien pasar el decimal a neperiano o viceversa. Seguiremos el proceso de escribir un solo logaritmo, sumando términos semejantes. Observe que la fórmula de cambio de base puede ser escrita como $$\log_b(m)=\frac {1} {\log_a(b)}\cdot \log_a(m) $$





   

Argumentos iguales, bases $e$ y 10


Ejemplo Resolver $\ln(x-2)=3-\log(x-2)$
Solución
Como aparece un término constante, 3, llevaremos la ecuación a la forma un logaritmo igual a constante. Trabajaremos con un solo tipo de logaritmo. Nosotros trabajaremos con el logaritmo natural, pero también se puede con el decimal. Pasamos el decimal a base e, usando la fórmula de cambio de base.
Se aplica la fórmula de cambio de variable al logaritmo decimal para escribirlo en términos de logaritmos neperianos
Al aplicar la fórmula de cambio de base, $ \log(x-2) =\frac{ \ln(x-2) }{\ln(10) }$ obtenemos la ecuaciòn
$$\ln(x-2)= 3-\frac{ 1 }{\ln(10) }\ln(x-2) $$

Se transforma la ecuación a la forma un logaritmo neperiano igual a constante
Pasamos todos los términos con logaritmos al lado izquierdo $$\ln(x-2)+ \frac{ 1 }{\ln(10) }\ln(x-2) = 3$$ Sacamos factor común $ \ln(x-2) $, (cuando los coeficientes son racionales, lo llamamos suma de términos semejantes) $$\left( 1+ \frac{ 1 }{\ln(10) } \right)\cdot \ln(x-2) = 3$$ $$\left( \frac{ \ln(10)+ 1 }{\ln(10) } \right)\cdot \ln(x-2) = 3$$ Pasamos el factor de $ \ln(x-2) $ a dividir. $$ \ln(x-2) =\frac{ 3} { \frac { \ln(10)+ 1 } {\ln(10) } } $$ Operamos el lado derecho $$ \ln(x-2) =\frac{ 3 \ln(10) } { \ln(10)+ 1 } $$ El lado derecho es un número real, el logaritmo que contiene la variable está despejado.

Se resuelve la ecuación resultante.

Nosotros la resolvemos pasando a la forma exponencial, la base es $e$, el exponente de la forma exponencial es el logaritmo. La ecuación queda $$ e^{ \frac{ 3 \ln(10) } { \ln(10)+ 1 } } =x-2 $$ Se resuelve esta última ecuación, es lineal, se despeja la variable $$x= e^{\frac{ 3 \ln(10) } { \ln(10)+ 1 }} +2$$

Se eliminan las soluciones que hagan algún argumento no positivo
La solución encontrada $x= e^{\frac{ 3 \ln(10) } { \ln(10)+ 1 }} +2$, se sustituye en $x-2$, los argumentos. La evaluación da como resultado $e^{\frac{ 3 \ln(10) } { \ln(10)+ 1 }} $, un número positivo, por tanto la solución encontrada en la ecuación anterior es la de la ecuación logarítmica dada.






Ejercicios Resolver
a) $\log_3(x+1)=\log_9(x+4)$
b) ${\small{\log_3(x+2)+\log_9(x+2)+\log_{81}(x+2)=1}}$
c) $\ln(x+3)=\log(x+3)$
d) $\log_{ \frac {1} {5} }(x)+\log_5(x)=\log_{25}(x)+1$
e) $2 \log_{ 2 }(x-5)-\log_{\sqrt{2} }(x+4)=0$

Respuestas
a) $3$; b) $3^{4/7}$ ; c) $-2$; d) $\frac { 1} { 25}$;
e) No tiene solución.
$x= \frac{1 }{2 }$ no tiene sentido en la ecuación original.





   


Resolviendo ecuaciones logarítmicas gráficamente


Si intentas resolver $$\log(x+3)-\log_2(x+1)=0$$ te podrás dar cuenta que la ecuación no puede ser resuelta con los métodos dados. Podemos entonces aproximar las soluciones por métodos gráficos.

La ecuación puede ser reescrita como $$\log(x+3)=\log_2(x+1)$$ Las soluciones de esta ecuación son los $x$´s de las soluciones, $(x,y)$, del sistema de ecuaciones $$\left\{\begin{matrix} y=\log(x+3) \\ \\ y=\log_2(x+1) \end{matrix}\right. $$ Entonces resolvemos el sistema de ecuaciones gráficamente.




Vamos a ver en el ejemplo cómo la ecuación puede ser resuelta gráficamente, paso a paso.

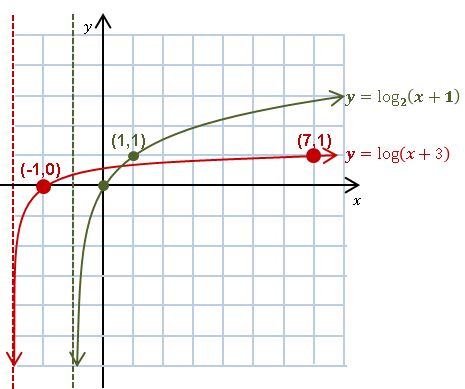
Ejemplo    Estimar las soluciones de $$\log(x+3)-\log_2(x+1)=0$$ Solución
Escribir la ecuación en la forma $f(x)=g(x)$ con $y=f(x)$ y $y=g(x)$ gráficos conocidos.


$$\log(x+3)=\log_2(x+1)$$

Graficar $y=f(x)$ y $y=g(x)$ en el mismo plano Cartesiano.

   

Encontrar los puntos de intersección.
   

Estimar la coordenada $x$ del punto(s) $(x,y)$ donde las gráficas se cortan. Ella es la solución(s) a la ecuación.

   

La solución que nosotros estimamos es $x\approx 0.5$



Recuerda En un sistema de ecuaciones, si las graficas no se cortan, entonces el sistema no tiene solución.

Ejemplo  Aproximar por métodos gráficos las soluciones de $$\log(x)-\log_2(x+2)-1=0$$ Solución
Reescribir la ecuación en la forma $f(x)=g(x)$ con $y=f(x)$ y $y=g(x)$ gráficos conocidos.


$$\log(x)=\log_2(x+2)+1$$

Graficar $y=f(x)$ y $y=g(x)$ en el mismo plano cartesiano.

   

Encontrar los puntos de intersección.
Las gráficas no se cortan.

Estimar la coordenada $x$ del punto(s) del punto, $(x,y)$, de intersección . La(s) coordenada(s) $x$ es la solución.

La ecuación no tiene solución porque las gráficas no se cruzan,






Usando Wolfram|Alpha.

Wolfram te permite encontrar una solución arpoximada usando métodos numericos

Find a approximate solution of the first example using Wolfram Alpha.

La solución aproximada al primer problema de graficación dado por Wolfram es $x\approx 0.45$


Tu puedes graficar múltiples funciones usando Wolfram Alpha Intenta el primer ejemplo usando Wolfram Alpha. Debes escribir $\log(10,x+3)$ para $f1$ y $\log(2,x+1)$ para $f2$.