FUNCIONES CUADRÁTICAS


Contenido
1 Función cuadrática y su gráfica 2 Completando cuadrados para graficar 3 Demostración de la fórmula del vértice 3 Graficar usando la fórmula del vértice 4 Método gráfico para resolver inecuaciones cuadráticas


FUNCIÓN CUADRÁTICA

Se establece la definición de función cuadrática. Se presenta la forma canónica de la función cuadrática, obteniendo la gráfica a través de transformaciones de la gráfica de la función $x$ al cuadrado, $f(x)=x^2$.

Ejercicios para después del video
Usando tranformaciones de gráficas, bosquejar la gráfica de cada una de las siguientes funciones
a) $f(x)=-x^2+1; \quad$
b) $ g(x)=\left (x-2 \right )^2-4; $
c) $h(x)= 2\left (x+1 \right )^2; \quad $
d) $ F(x)=-2 \left (x-3 \right )^2+2 $

Haz clic para ver las respuestas

Respuestas


Respuestas







   


CÓMO LLEVAR LA FUNCIÓN CUADRÁTICA A SU
FORMA CANÓNICA

Cuando la función está en la forma $f(x)=a(x-h)^2+k$ se puede graficar rápidamente. En el video se muestra, mediante un ejemplo, cómo llevar una función que no está en este forma, a esta forma y de allí graficar. En el proceso se usa la técnica de completación de cuadrados.




Ejercicios
Lleve cada función dada a la forma $f(x)=a(x-h)^2+k$. Luego, usando tranformaciones de gráficas, trace la gráfica
$ a) \; y=-x^2+2x; $
$b) \; y=2x^2+3; $
$) \; y= 2x^2+6x+6; $
$ d) \; y= -2x^2-5x-1 $
Respuestas
$a)\; y=-(x-1)^2+1\qquad\qquad \qquad$ $b) \; y=2x^2+3$
Respuestas

$c)\; y=2(x-\frac{3}{2})^2+\frac{3}{2}\qquad\qquad $ $d) \; y=-2(x+\frac{5}{4} )^2+\frac{17}{8}$


   


DEMOSTRACIÓN DE LA FÓRMULA DE LA COORDENADA $x$ DEL VÉRTICE

Se presenta la forma canónica de la función cuadrática, obteniendo la gráfica a través de transformaciones de la gráfica de la función $x$ al cuadrado. Para poder realizar este proceso en cualquier función cuadrática hay primero que llevarlo a la forma canónica de una función cuadrática usando la técnica de completación de cuadrados. Se realiza el proceso de llevar la forma general a la forma canónica, estableciendo la coordenada $x$ del vértice.






   


GRÁFICAR UNA FUNCIÓN CUADRÁTICA USANDO LA FÓRMULA DEL VÉRTICE

Usando la fórmula de la coordenada $x$ del vértice en términos de los coeficientes de la forma general, se consigue la gráfica de una función cuadrática de una manera rápida. En este proceso se toma en cuenta el signo de $a$, el coeficiente principal, que establece el sentido de la parábola. Para graficar con mayor precisión se determinan las intersecciones con los ejes y se toma en cuenta que la gráfica es simétrica con respecto a la recta vertical que pasa por el vértice

Ejercicio para después del video
Para cada una de las siguientes funciones, consiga las intersecciones con los ejes, el vértice, el eje de simetría y el sentido de la parábola. Finalmente, graficar, tomando en cuenta las informaciones halladas
$ a) \; y=x^2-6x+8; $
$b) \; y=-2x^2+6x; $
$c) \; y= 2(x-3)^2+4(x-2); $
$d) \; y= -2(x-2)(x+4) $


Respuestas
$a) \; $ Cortes con los ejes $(4,0) (2,0)$ y $(0,8)$
Vértice $ (3,-1)$
Eje de simetría $x=3$
$a=1$, la parábola abre hacia arriba



Respuestas

$b) \; $ Cortes con los ejes $(0,0) $ y $(3,0)$
Vértice $ (\frac{3 }{ 2}, \frac{9 }{ 2} )$
Eje de simetría $x= \frac{3 }{ 2} $
$a=-2$, la parábola abre hacia abajo



Respuestas

$c) \; y=2x^2-8x+10 $
Corte solo con el eje $y$, $(0,10)$
Vértice $ (2,2)$
Eje de simetría $x=2$
$a=2$, la parábola abre hacia arriba



Respuestas

$d) \; y=-2x^2-4x+16$
Cortes con los ejes: $(2,0),(-4,0)$ y $(0,16)$
Vértice $ (-1,16)$
Eje de simetría $x=-1$
$a=-2$, la parábola abre hacia abajo








   


MÉTODO GRÁFICO PARA RESOLVER UNA INECUACIÓN CUADRÁTICA

En el enlace podrás ver el documento en pdf que muestra cómo se resuelve una desigualdad cuadrática en una sola variable a través de un procedimiento geométrico. La gráfica de la función ayuda a determinar el conjuntos de las $x$ solución de una desigualdad.
Documento en PDF
Ejercicio para después del video
Resuelva cada inecuación cuadrática por el método gráfico
$a) \; -x^2+4>0; $
$ b)\; -x^2-x+6\geq 0 $
$ c) \; x^2+5x+6>0; \; \; \; $
$ d)\; x^2+3x+1\leq 0$
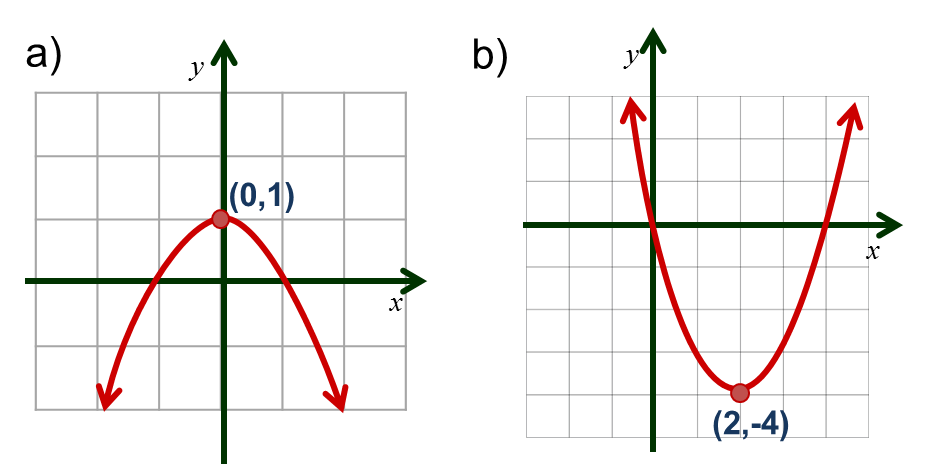
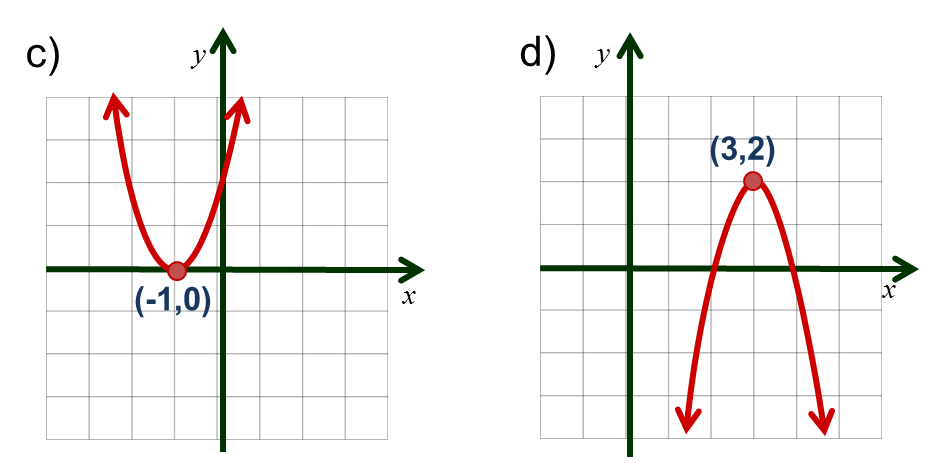
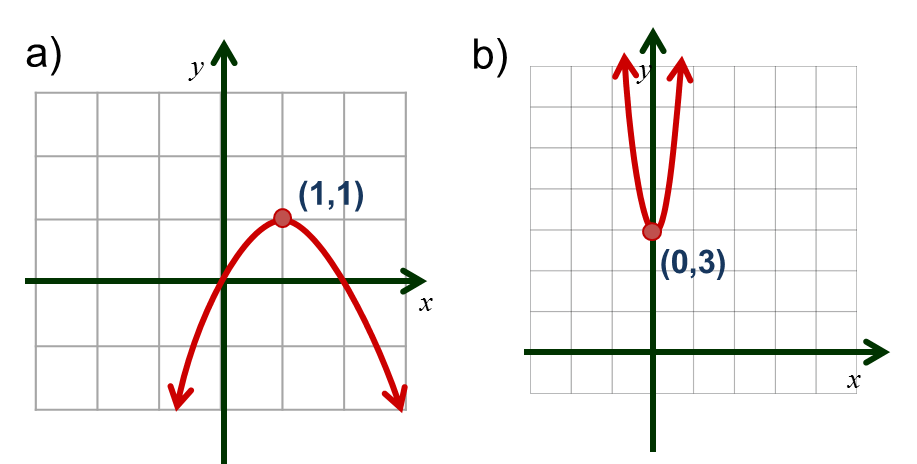
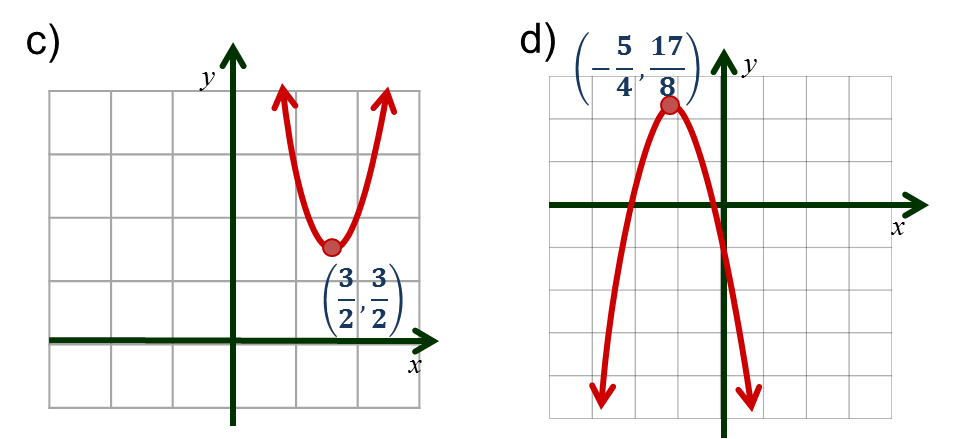
Respuestas
$ a) \; (-2,2)$   $ b) \; [-3,2]$  
$ c) \; (-\infty,-3)\cup (-2,\infty)$   $ d) \; [ \frac { -3-\sqrt{5} } { 2 } , \frac { -3+\sqrt{5} } { 2 } ]$