Dominio de funciones logarítmicas y de funciones que las contienen
Como la función exponencial $f(x)=b^x$ tiene como inversa la función logarítmica $f^{-1}=\log_b(x)$, se tiene que
Dominio de la función logaritmica = Rango de la función exponencial.
Como el rango de la función exponencial $=(0,\infty)$ Tenemos que
Esto es válido para cualquier base permitida. El dominio de la función logaritmo neperiano, o decimal, o de base por ejemplo $1/2$, es $(0,\infty)$.
Así pues, sólo tiene sentido evaluar logaritmos en números positivos. El argumento del logaritmo debe ser mayor que 0.
La función $g(x)=\log(x-3)$ no está definida en $x=1$, pues el argumento del logaritmo, $1-3=-2$, es un número negativo. $x=1$ no está en el dominio de la función $g$.
Como el rango de la función exponencial $=(0,\infty)$ Tenemos que
Esto es válido para cualquier base permitida. El dominio de la función logaritmo neperiano, o decimal, o de base por ejemplo $1/2$, es $(0,\infty)$.
Así pues, sólo tiene sentido evaluar logaritmos en números positivos. El argumento del logaritmo debe ser mayor que 0.
La función $g(x)=\log(x-3)$ no está definida en $x=1$, pues el argumento del logaritmo, $1-3=-2$, es un número negativo. $x=1$ no está en el dominio de la función $g$.
(Verifica que la calculadora te manda un mensaje de error cuando quieres calcular $\log(1-3)$.)
Dada una función con logaritmos, se quiere determinar el conjunto de todos los números reales donde la función está definida y es un número real, esto es, se quiere hallar el dominio de la función. Esto lo podemos establecer de dos maneras: por medio de la gráfica de la función y analíticamente.Determinación del dominio por medio de su gráfica
Para determinar el dominio por medio de la gráfica de la función: Se proyecta cada punto sobre el eje $x$.El intervalo proyectado en el eje x es el dominio de la función.
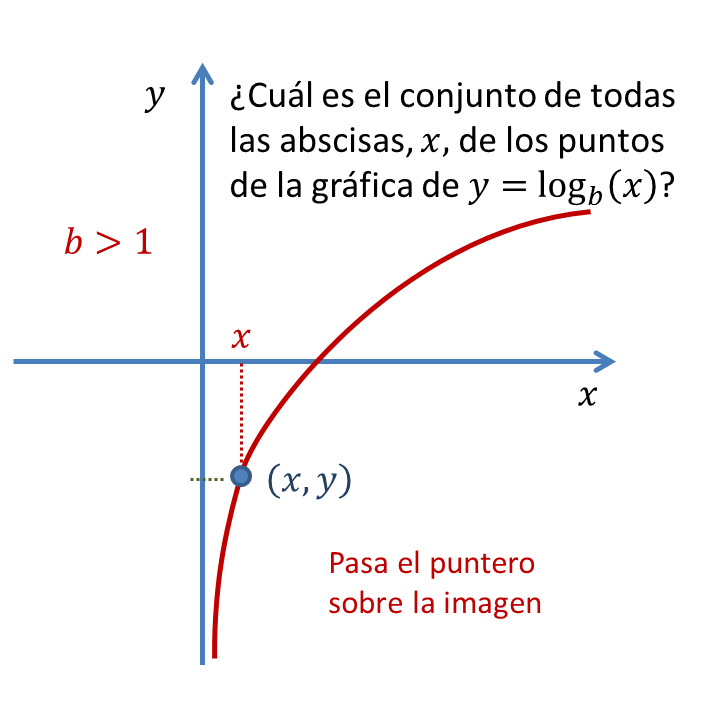 Se puede ver que los puntos que conforman el gráfico de la función logarítmica corresponden
a puntos con abscisas positivas y para cualquier $ x$ positivo, hay un punto de la gráfica con esta abscisa.
Ejemplo
Se puede ver que los puntos que conforman el gráfico de la función logarítmica corresponden
a puntos con abscisas positivas y para cualquier $ x$ positivo, hay un punto de la gráfica con esta abscisa.
Ejemplo
A la función $g(x)=\log(x-3)$ le podemos hallar su dominio de manera geométrica, pues la gráfica de la función puede ser obtenida por una traslación hacia la derecha de la gráfica de $y=\log(x)$
Determinación del dominio analíticamente
No toda función con logaritmos se le puede graficar tan fácilmente, incluso se puede requerir el dominio para determinar la gráfica. En lo que sigue se hallará el dominio de funciones con logaritmos analíticamente, esto es, a través del planteamientos y resolución de ecuaciones e inecuaciones y operaciones conjuntista entre los conjuntos solución encontrados. Empecemos por la función sencilla planteada. Ejemplo Determinar el dominio de $ \ g(x)=\log(x-3)$ Solución Plantear la inecuación ARGUMENTO DEL LOGARITMO $ >0$.
Recuerda que si una función puede ser interpretada como una suma, diferencia o producto de dos funciones $f=(f_1+f_2)$, entonces el dominio puede ser calculado determinando el dominio de $f_1$ y de $f_2$, para luego interceptarlos.
A continuación presentamos un ejemplo de una función que puede ser interpretada como la suma de dos funciones.
Ejemplo
Halle el dominio de $ \ f(x)=\sqrt{3-x} +\ln(x) $.
Solución
La función puede ser vista como la suma de dos funciones
$$f_1(x)=\sqrt{3-x} \; \text{ y } \; f_2(x)=\ln(x)$$
Determinar el dominio de $f_1$
Determinar el dominio de $f_2$
Se toma la intersección, la parte común, de los conjuntos determinados en 1 y 2
Concluir, señalando cuál es el dominio de la función
El dominio de funciones diferencias o productos son similares a las de funciones suma.
Ejercicios Encuentre el dominio de cada una de las siguientes funciones a) $f(x)=x\ln(x+2)$; b) $g(x)=\frac{x-3}{x-1}+\ln(x+2)$; c) $h(x)=\sqrt{x^2-1}+\ln(-x)$;
El dominio de funciones diferencias o productos son similares a las de funciones suma.
Ejercicios Encuentre el dominio de cada una de las siguientes funciones a) $f(x)=x\ln(x+2)$; b) $g(x)=\frac{x-3}{x-1}+\ln(x+2)$; c) $h(x)=\sqrt{x^2-1}+\ln(-x)$;
Funciones cocientes
Para funciones que pueden ser interpretadas como el cociente de dos funciones,
$f=\frac{f_1}{f_2}$, hay que hacer una consideración adicional: que los valores de la función del
denominador sean distintos de cero. Entonces el dominio puede ser calculado determinado el dominio
de $f_1$ y de $f_2$, luego interceptarlos y quitarle los $x$ donde el denominador se anule.
Ejemplo Halle el dominio de $ f(x)=\frac{x^2-4}{\ln(x-1)-5} $ Solución La función puede ser vista como el cociente de funciones
Determinar el dominio de $f_2$
Se toma la intersección, la parte común, de los conjuntos determinados en los pasos 1 y 2
Quitar al conjunto anterior los $x$ donde el denominador se hace 0.
Ejercicios Encuentre el dominio de cada una de las siguientes funciones
a) $ f(x)= \frac{ \ln (x+1) } {x-3} $;
b) $g(x)=\frac{x-4}{\ln(x-2)}$;
c) $h(x)= \frac{ \sqrt{1-x^2}}{\ln(-x)}$;
Ejemplo Halle el dominio de $ f(x)=\frac{x^2-4}{\ln(x-1)-5} $ Solución La función puede ser vista como el cociente de funciones
$ f_1(x)=x^2-4 $ entre $f_2(x)=\ln(x-1)-5 $
Determinar el dominio de $f_1$
Composición de funciones con logaritmos
El dominio de funciones compuestas del tipo $\log_b(g(x))$ es el conjunto de las $x$ para las cuales
$g(x)>0$ y $x\in Dom\ g$. Esto es para cualquier base. En notación de conjunto
En el siguiente ejemplo trabajaremos con logaritmos naturales o neperianos, de base $e$. Ejemplo Halle el dominio de $ \ f(x)=\ln(x^2-3x-4) $ Solución La función puede ser vista como la composición de dos funciones. Se determina el dominio de la función interna,
Se determinan las $x$ para las cuales el argumento del logaritmo es mayor a 0
Se toma la intersección, la parte común, de los conjuntos determinados en 1 y 2
Concluir, señalando cuál es el dominio de la función
En el siguiente ejemplo tenemos una función logaritmo de una función que contiene otro logaritmo, una función compuesta del tipo $\ln(h)$
Ejemplo
Halle el dominio de $f(x)=\ln(\ln(x)+1) $
Solución
La función puede ser vista como la composición de dos funciones.
Se determina el dominio de la función interna,
Se determinan las $x$ para las cuales el argumento del logaritmo es mayor a 0
Se toma la intersección, la parte común, de los conjuntos determinados en los pasos 1 y 2
Concluir, señalando cuál es el dominio de la función
En el siguiente ejemplo tenemos una función que es la raíz de una función que contiene logaritmo, una función compuesta del tipo $\sqrt{h}$. El dominio es el conjunto de las $x$ para las cuales $h(x)\geq 0$ y $x\in Dom\ h$.
Ejemplo
Halle el dominio de $f(x)=\sqrt{2-\ln(x)} $
Solución
Se determina el dominio de la función interna,
Se determinan las $x$ para las cuáles el radicando es mayor o igual a 0
Se toma la intersección, la parte común, de los conjuntos determinados en 1 y 2
Concluir, señalando cuál es el dominio de la función
En el siguiente ejemplo trabajaremos con logaritmos naturales o neperianos, de base $e$. Ejemplo Halle el dominio de $ \ f(x)=\ln(x^2-3x-4) $ Solución La función puede ser vista como la composición de dos funciones. Se determina el dominio de la función interna,



 Vemos que la intersección, la parte común es
$$(0,3]$$
Vemos que la intersección, la parte común es
$$(0,3]$$
 3) Tomamos valores de prueba en cada intervalo y los evaluamos en el polinomio $x^2-3x-4$. Se anota el signo resultante.
3) Tomamos valores de prueba en cada intervalo y los evaluamos en el polinomio $x^2-3x-4$. Se anota el signo resultante.
 4) Se concluye. Como la desigualdad es del tipo $>0$, el conjunto solución de la desigualdad planteada es la unión de los intervalos donde la evaluación resultó positiva.
Esto es $$(-\infty,-1)\cup (4,\infty)$$
En este conjunto el argumento del logaritmo es positivo.
4) Se concluye. Como la desigualdad es del tipo $>0$, el conjunto solución de la desigualdad planteada es la unión de los intervalos donde la evaluación resultó positiva.
Esto es $$(-\infty,-1)\cup (4,\infty)$$
En este conjunto el argumento del logaritmo es positivo.

 Vemos que el logaritmo es mayor que $-1$ a partir de la $x$ en que $\ln(x)=-1$.
Al resolver esta ecuación encontramos que
$$x=e^{-1}$$
En definitiva, $$\ln(x)+1>0 \text{ si y solo si } x\in (e^{-1},\infty)$$
Vemos que el logaritmo es mayor que $-1$ a partir de la $x$ en que $\ln(x)=-1$.
Al resolver esta ecuación encontramos que
$$x=e^{-1}$$
En definitiva, $$\ln(x)+1>0 \text{ si y solo si } x\in (e^{-1},\infty)$$
 Vemos que la intersección, la parte común es
$ {\small {\{ x | \; \ln(x)+1>0\} \cap Dom \left (\ln(x)+1 \right ) }}$ $\;{\small { =
(e^{-1},\infty)}}$
Vemos que la intersección, la parte común es
$ {\small {\{ x | \; \ln(x)+1>0\} \cap Dom \left (\ln(x)+1 \right ) }}$ $\;{\small { =
(e^{-1},\infty)}}$
 Vemos que el logaritmo es menor o igual a $2$ antes de la $x$ en que $\ln(x)=2$.
Al resolver esta ecuación encontramos que
$$x=e^{2}$$
En definitiva, $$2-\ln(x)\geq 0 \text{ si y solo si } x\in (0,e^{2}]$$
Observe que ya estamos considerando el dominio de $\ln(x)$. Así que el paso 3 no haría falta, sin embargo, para ser metódicos lo consideramos
Vemos que el logaritmo es menor o igual a $2$ antes de la $x$ en que $\ln(x)=2$.
Al resolver esta ecuación encontramos que
$$x=e^{2}$$
En definitiva, $$2-\ln(x)\geq 0 \text{ si y solo si } x\in (0,e^{2}]$$
Observe que ya estamos considerando el dominio de $\ln(x)$. Así que el paso 3 no haría falta, sin embargo, para ser metódicos lo consideramos