FUNCIÓN UNO A UNO
PRUEBA DE LA RECTA HORIZONTAL

FUNCIÓN INVERSA


Se ha estudiado cuando una ecuación en $x$ y $y$ define a $y$ como función de $x$.
En este caso tenemos la función inversa de la primera. No toda función definida a través de una ecuación tiene función inversa.

El concepto de función uno a uno (biunívoca, inyectiva) es clave para definir la función inversa de una función dada. Se establece el criterio o prueba de la recta horizontal para determinar si la función es o no uno a uno.

Se propone una sucesión de pasos para obtener la inversa. La gráfica de la función inversa de $f$ puede ser obtenida a partir de la gráfica de la función f reflejando esta última en la recta $y=x$.

Contenido
1 Prueba de la recta horizontal. Función 1 a 1 2 Cómo obtener la función inversa 3 Gráfica de la función inversa

Video 1
PRUEBA DE LA RECTA HORIZONTAL.
FUNCIÓN UNO A UNO (BIUNIVOCA)

Se estudia cuando una función tiene o no inversa. Para verificar si una función tiene o no función inversa se propone la prueba de la recta horizontal. Se establece la definición de función uno a uno.






   



Video 2
CÓMO OBTENER LA FUNCIÓN INVERSA.
EJEMPLO

Se recomiendan una serie de pasos para obtener la función inversa de una función dada.
Se desarrolla un ejemplo para obtener la función inversa de una función dada siguiendo los pasos recomendados.






Ejercicio para después del video.- Determinar, si existe, la función inversa de cada una de las siguientes funciones:
a) $f(x)=x^2+1\;$     b) $g(x)=\frac{2 }{ x}$    
c) $h(x)=\left ( x-1 \right )^3$

Pulsa el botón para ver las respuestas


Respuestas
a) No tiene inversa
b ) $g^{-1}(x)=\frac{2 }{ x}$     c) $h^{-1}(x)=\sqrt[3]{x}+1 $




   


Video 3
GRÁFICA DE LA FUNCIÓN INVERSA

Recuerde que la gráfica de la función $y=f (x+c)$ puede ser obtenida a partir de la gráfica de $f$.

La cuestión ahora es: si $f$ tiene función inversa, ¿se puede obtener la gráfica de la función inversa a partir de la gráfica de $f$ ?

Un ejemplo es resuelto paso a paso dando recomendaciones de trabajo.




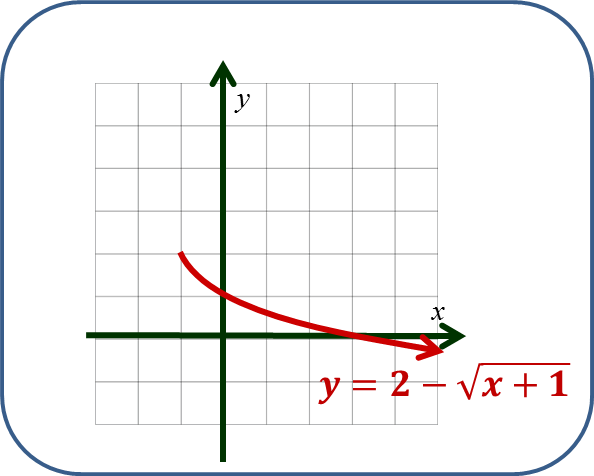
Ejercicio para después del video.-Determinar la función inversa de f. Grafique la función y su inversa en el mismo plano.
$ f\left( x \right)=2-\sqrt{x+1}$

Respuesta
$f^{-1}(x)=\left ( x-2 \right )^2-1$
Pasa el puntero sobre la imagen para ver las dos funciones.