FUNCIONES CONCEPTOS
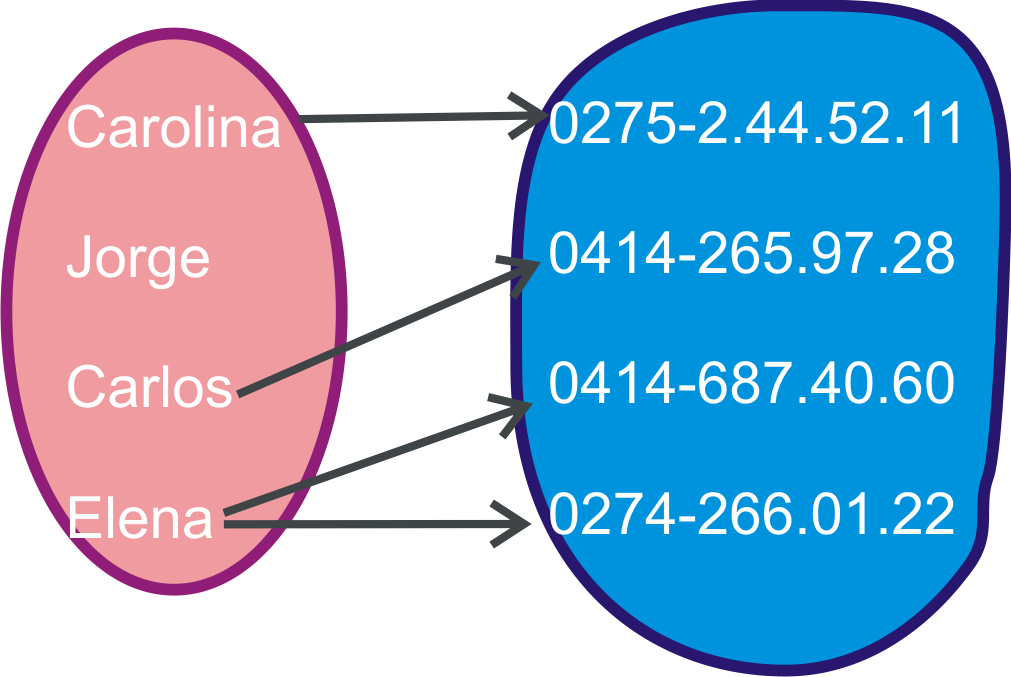
Podemos encontrar muchas relaciones entre dos conjuntos. Por ejemplo un conjunto puede ser los compañeros de una materia en el semestre y el otro conjunto el de los posibles números telefónicos. Existe una relación natural del conjunto de personas al conjunto de números telefónicos: la que asocia a cada persona sus números telefónicos. Este tipo de relación no nos va interesar. Pues puede suceder que a cada persona le corresponda dos números telefónicos o una persona no tenga número telefónico. Una función es una relación especial entre dos conjuntos.
FUNCIONES. CONCEPTOS
Se presenta el concepto de función, defniendo los elementos que conforman una función: El dominio, el conjunto de llegada y la regla. Se explican los conceptos de rango, imagen. Se presentan ejemplos de relaciones de la vida real que son funciones y otros ejemplos que no son funciones
Ejercicios para después del video 1) ¿Por qué la relación entre el conjuntos formado por Carolina, Jorge, Carlos y Elena y el conjunto de números telefónicos dado, no define una función?
Haz clic para ver la respuesta.
2) Diga cuáles de las siguientes relaciones define una función
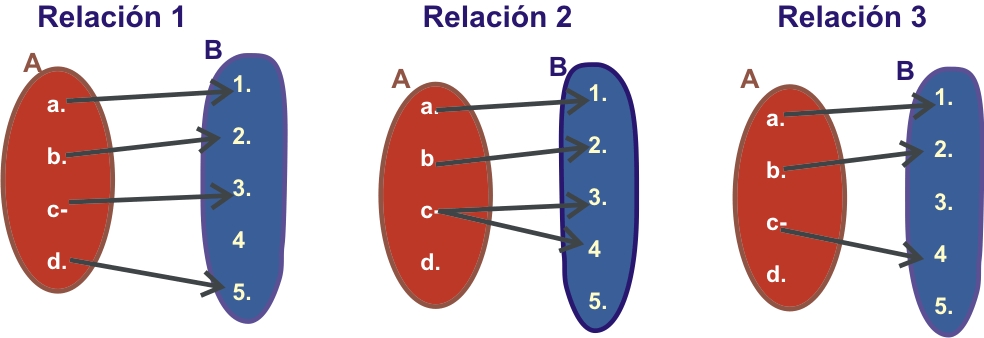
Respuestas 2:
FUNCIONES REALES DE VARIABLE REAL
La definición es presentada en el video. Tambien se verá el significado de variable independiente y dependiente. ¿Cómo se puede presentar la definición de una función? Al final del video se explica la notación funcional de funciones. Se usa esta notación para representar los valores de la función. Recuerde f (2) representa la imagen de 2 mediante f. Una variable es un símbolo que sirve para representar los elementos de un conjunto. La variable que representa los valores del dominio se llama variable independienteRecuerde f (2) representa la imagen de 2 mediante f. Una variable es un símbolo que sirve para representar los elementos de un conjunto. La variable que representa los valores del dominio se llama variable independiente
