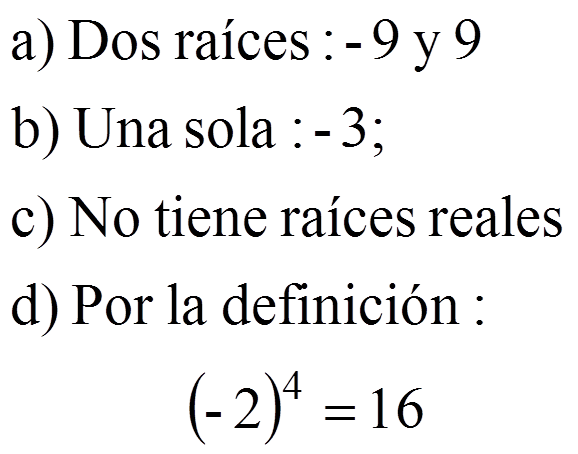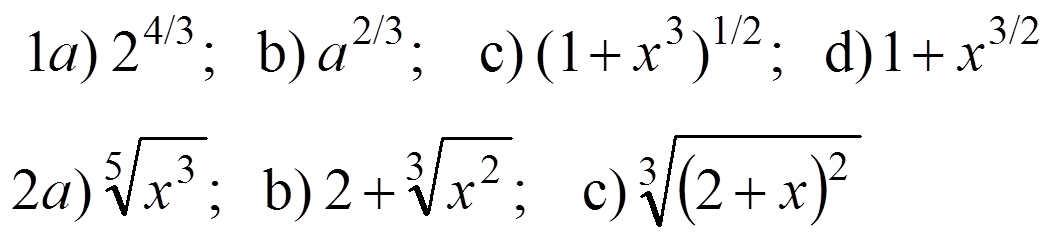RADICALES  Y  
EXPONENTES  RACIONALES

VIDEO 1
Definición de la raíz n-ésima de un número.
Caso n par y n impar

a) ¿Cuántas raíces cuadradas tiene 81?
b) ¿Cuántas raíces cúbicas tiene -27?
c) ¿Cuántas raíces cuadradas tiene -4? ¿Cuáles son estas raíces?
d) ¿Cómo podemos justificar que -2 es una raíz cuarta de 16?

En este video no sólo se establece el concepto de raíz de un número, además se dan precisiones fundamentales.




Ejercicios para después del video
1) Conteste cada una de las preguntas formuladas

Pulsa el botón para ver las respuestas




En $b^n=a$ para $a$ positivo y $n$ un número par, se tiene dos números reales, $b$, que satisfacen esta identidad, uno positivo y otro negativo, el primero llamado la raíz positiva o principal de a y el segundo la raíz negativa, denotadas respectivamente por

$\sqrt[n]{a}\quad$ y $\quad-\sqrt[n]{a}$


Así, podemos expresar las raíces cuartas de 7 como

$\sqrt[4]{7}\quad$ y $\quad-\sqrt[4]{7}$


La expresión $\sqrt[n]{a}\;$ indica la raíz n-ésima principal de $a.$ Esta expresión se llama expresión radical.

En el diagrama indicamos las partes del radical.






   

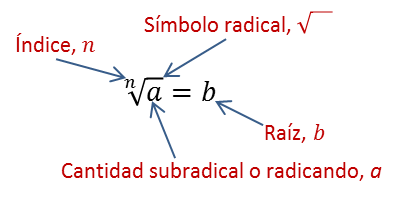
VIDEO 2
PARTES DE UN RADICAL. NOTACIÓN

Se establecen las partes de un radical: índice, radicando, signo radical, dando consejos de escritura. Se trata el caso de la raíz de una potencia con exponente igual al índice, viendo la relación entre el radical y el valor absoluto.


Recuerda, no vale la simplificación en el caso que el índice sea par. Un ejemplo te lo confirma. Calcula $\sqrt{(-2)^2}$, recuerda que primero determinas el radicando y luego, obtienes la raíz de este resultado. Relaciona el resultado con –2.

$\sqrt{(-2)^2}=\sqrt{4}=2$
El resultado es –( –2), el valor absoluto de –2.


Ejercicio para después del video
1) Simplifique $\sqrt[4]{x^{12}}$

Pulsa el botón para ver cómo resolver el ejercicio

Se expresa el radicando como una potencia de grado igual al índice de la raíz. Para eso se usa la regla de la potencia de una potencia $\sqrt[4]{x^{12}}=\sqrt[4]{(x^{3})^4 }=|x^3|$






   

PRINCIPALES PROPIEDADES DE LOS RADICALES

Asuma que cada radical existe.
La propiedades normalmente se refieren por el lado izquierdo de la igualdad.

Raíz de un producto $$\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}$$
La raíz de un producto es el producto de las raíces.
Algunas aplicaciones de esta regla, con ejemplos

Raíz de un cociente $$\sqrt[n]{\frac{a}{b} }=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}$$
Raiz de un cociente es el cociente de las raíces.
Algunas aplicaciones de esta regla, con ejemplos


Raíz de una raíz $$\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}$$
Raiz de una raíz es la raíz con el mismo radicando e índice el producto de los índices.
Algunas aplicaciones de esta regla, con ejemplos

De la propia definición de la raíz n-ésima de a se tiene la siguiente
Potencia de una raíz, exponente igual al índice,
$$(\sqrt[n]{a})^n=a$$

Raíz de una potencia, con índice igual al exponente.
Hay que diferenciar dos casos.
n impar:   $\sqrt[n]{a^n}=a$
   Ejemplo   $\sqrt[3]{5^3}=5$

n par:   $\sqrt[n]{a^n}=|a|$
   Ejemplo    $\sqrt[6]{(-5)^6}=|-5|=5$


   

VIDEO 3
EXPONENTES RACIONALES

Frecuentemente se trabajarán con exponentes fraccionarios en Cálculo. En este video se da la definición. Se muestran ejemplos, que surgen en las Matemáticas superiores, de cómo pasar de la notación con radicales a la notación con exponentes fraccionarios, también se muestra el proceso inverso


Ejercicios para después del video
1) Pase a la notación de exponente racional.


2) Reescriba la expresión usando un radical. No use exponentes negativos, ni racionales
a) $x^{3/5};\quad$ b) $2+x^{2/3};\quad$ c) $(2+x)^{2/3};\quad$




   

VIDEO 4
EXPONENTES RACIONALES

La definición de exponentes racionales es ampliada para cuando la base es un número positivo. Se justifica porque esta nueva definición no sirve en el caso que la base sea un número negativo. Se muestra un primer ejemplo de cómo al pasar a la notación con exponente fraccionario podemos simplificar un radical.


Ejercicioa para después del video
1) Simplifique pasando a la notación de exponente racional
a) $\sqrt[3]{2^{12}};\quad$ b) $\sqrt[5]{3^{20}};\quad$ c) $\sqrt[6]{2^{18}}$
a) 16;   b) $3^4=81;$   c) 8


Ejercicios para después del video
1) Escriba como un solo radical
a) $\sqrt{3}\sqrt{10};\quad$ b) $\dfrac{\sqrt{6}}{\sqrt{3}}$

2) Aplicando propiedades de radicales, simplifique las siguientes expresiones.
a) $\sqrt{3}\sqrt{12};\quad$ b) $\dfrac{\sqrt{8}}{\sqrt{2}}; $ c) $\dfrac{\sqrt{12}\sqrt{6}}{\sqrt{2}}$
1a) $\sqrt{30};\quad$ b) $\sqrt{2}$
2a) 6;  b) 2;   c) 6




   

VIDEO 5
CÁLCULO DE ALGUNAS EXPRESIONES CON RADICALES NUMÉRICOS USANDO LAS LEYES DE LOS RADICALES

Algunos radicales numéricos pueden ser calculados usando propiedades algebraicas y de radicales. En el video se muestran algunos ejemplos.


Ejercicios para después del video
1) Determine
a) $\sqrt[3]{-27.000};\quad$ b) $\sqrt{0.04}$
a) $-30;\quad$ b) $0.2$