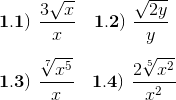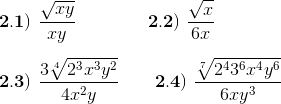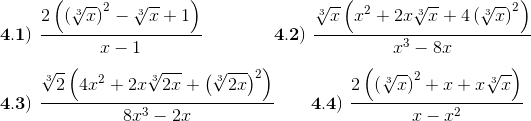Racionalización de denominadores
Factor racionalizante
Un procedimiento general para conseguir la racionalización del denominador es multiplicar numerador y el denominador por un mismo factor.
El tipo de expresión que se multiplica el numerador y el denominador depende en primer lugar del número de términos del denominador.
Primero se estudiará el caso en que el numerador es un monomio, luego el caso en que es un binomio, para finalmente tratar el caso de trinomio con raíces cuadradas.

VIDEO 1
RACIONALIZACION DE DENOMINADORES.
CASO MONOMIO
El video explica el concepto de la racionalización de denominadores, mostrando su importancia y dando ideas generales para llevar este proceso. Se muestran procedimientos para llevar a cabo la racionalización en el caso que el denominador sea un monomio, explicando cómo obtener el factor racionalizante.
¿Puede existir varios factores racionalizantes? Abajo te mostramos como racionalizar el denominador de una expresión de dos maneras, explicándote los dos procedimientos paso a paso. Cada procedimiento usa distintos factores racionalizantes.
Ejemplo
Racionalizar el denominador de $$\dfrac{3}{\sqrt[5]{4^2}}$$
Primer procedimiento Factor racionalizante dado por el propio denominador de la expresión
Segundo procedimiento Se expresa el radicando como producto de sus factores primos. Se puede considerar simplificar el radical. Muchas veces la expresión racionalizadora es distinta a la del primer procedimiento.
Haz clic para ver el desarrollo paso a paso.
Ejercicios 1) Racionalice el denominador
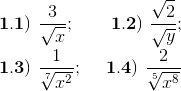
Pulsa el botón para ver las respuestas
VIDEO 2
DENOMINADOR ES UN MONOMIO.
EJEMPLOS MÁS COMPLICADOS
Se considera el caso en que el denominador es un monomio con una radicando que es un producto y el índice de la raíz mayor a dos. Se explica cómo obtener la expresión racionalizante o racionalizadora.
Ejercicios para después del video
2) Racionalice el denominador en cada expresión
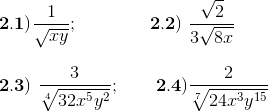
Pulsa el botón para ver las respuestas
VIDEO 3
RACIONALIZAR DENOMINADORES
CASO BINOMIOS CON SÓLO RAÍCES CUADRADAS
Se considera denominadores que son una suma o una resta con solamente raíces cuadradas. La expresión racionalizante en este caso es la conjugada del denominador, pues ella provoca el producto de una suma por su diferencia.
Ejercicios
Racionalice el denominador en cada expresión.
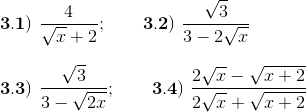
Ejercicios
Indica si la expresión del denominador es un monomio o un binomio.
Señala el factor racionalizante.
Finalmente, escribe cada expresión con el denominador racionalizado.
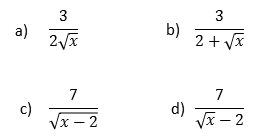
Pulsa el botón para ver las respuestas
VIDEO 5
RACIONALIZAR DENOMINADORES.
TRINOMIO CON RAÍCES CUADRADAS
En el caso que se tenga tres términos, con un solo radical, se reordena y se asocia convenientemente para interpretar el denominador como una suma o una diferencia de dos términos y así poder usar la conjugada para racionalizar el denominador.
En la animación se muestra cómo en ocasiones conviene reordenar para hacer factible este proceso.
Ejercicios para después del video
5) Racionalice el denominador en cada expresión
Pulsa el botón para ver las respuestas
RACIONALIZAR DENOMINADORES.
BINOMIOS CON SÓLO RAÍCES CÚBICAS
En el caso que el denominador tenga dos términos con solamente raíces cúbicas se usa las factorizaciones de diferencia y de suma de cubos para buscar un factor racionalizante.
$$a^3+b^3= (a+b)(a^2-ab+b^2) $$
$$a^3-b^3=(a-b)(a^2+ab+b^2)$$
Se explica el concepto de términos semejantes aplicado a expresiones algebraicas, mostrando varios ejemplos. Se muestra cómo sumar términos semejantes justificada por la propiedad distributiva. Se simplifica expresiones algebraicas, en el sentido que se reducen los términos semejantes. Se muestran ejemplos de sumas y restas de expresiones algebraicas. Se simplifican radicales con el objeto que aparezcan términos semejantes. Ejercicios para después del video
4) Racionalice el denominador en cada expresión
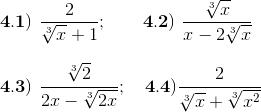
Pulsa el botón para ver las respuestas