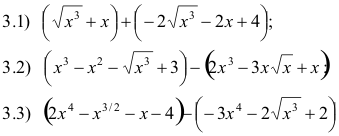EXPRESIONES ALGEBRAICAS Y POLINOMIOS
CONCEPTOS
SUMAS Y RESTAS
VIDEO 1 EXPRESIONES ALGEBRAICAS. DEFINCIONES
Los distintos elementos del lenguaje algebraico son explicados en el video empezando por la propia definición de expresión algebraica, considerando la radicación como una operación que puede estar en una expresión algebraica. Se discute sobre el concepto de variables y constantes literales.Se analizan expresiones de acuerdo al número de términos, se define el coeficiente numérico de un término. Se explica el concepto de coeficiente de un término con ejemplos. La definición estricta de monomio, binomio y trinomio es establecida, ampliando la definición para términos que contienen expresiones distintas a potencias. Se introduce la definición de polinomio y la necesidad del concepto de multinomio para referirse a expresiones con más de tres términos en que salvo el coeficiente numérico se presentan términos con expresiones distintas a potencias con enteros no negativos en la variable.
VIDEO 2 POLINOMIOS. DEFINICIONES
Se establece la definición de un polinomio, mostrando ejemplos que son y otros que no son polinomios. Otras definiciones como el grado del polinomio, el coeficiente principal, el término independiente son tratadas en el video. También la clasificación de los polinomios de acuerdo al número de términos. Se revisan los conceptos de forma canónica y forma completa de un polinomio.
Ejercicios para después del video
1) Diga cuáles de las siguientes expresiones son polinomios. Para las expresiones polinómicas diga el grado, el coeficiente principal, el coeficiente de grado 2 y clasifique el polinomio de acuerdo al número de términos.
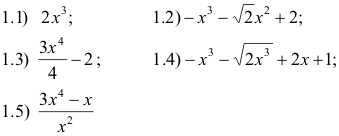
VIDEO 3
SIMPLIFICAR POLINOMIOS EN UNA VARIABLE
REDUCIR TÉRMINOS SEMEJANTES
Se explica qué son términos semejantes y cómo se reducen. En el caso de polinomios en una sola variable son los términos con la misma potencia en la variable, que tienen la misma parte literal. La redución de términos semejantes se fundamente en la propiedad distributiva. Se puede proceder mentalmente: sumando los coeficientes y dejando la misma parte literal.
Se simplifica polinomios reduciendo términos semejantes. En el video se justifica paso a paso la simplificación de
polinomios. Luego, se dan recomendaciones para hacerlo
en una sola igualdad: Identificando los términos semejantes, de mayor a menor grado, y reduciéndolos.
SUMA Y RESTA DE POLINOMIOS
MÉTODO HORIZONTAL
El método horizontal simplemente consiste en eliminar paréntesis y reducir términos
semejantes. $(x^3-4x-2)-(3x^3-2x^2+x)$
$={\color{Red} {x^3}}{\color{Blue} {-4x}}-2{\color{Red} {-3x^3}}{\color{Teal} {+2x^2}}{\color{Blue} {-x}}$
$={\color{Red} {-2x^3}}{\color{Teal} {+2x^2}}{\color{Blue} {-5x}}-2$
Ejercicios
2) Efectúe y simplifique
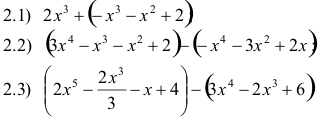
VIDEO 5 SUMAS Y RESTAS DE EXPRESIONES ALGEBRAICAS REDUCIR TERMINOS SEMEJANTES
Generalizaciones de la reglas de la potencia de un producto y de la potencia de un cociente Se explica el concepto de términos semejantes aplicado a expresiones algebraicas, mostrando varios ejemplos. Se muestra cómo sumar términos semejantes justificada por la propiedad distributiva. Se simplifica expresiones algebraicas, en el sentido que se reducen los términos semejantes. Se muestran ejemplos de sumas y restas de expresiones algebraicas. Se simplifican radicales con el objeto que aparezcan términos semejantes.Ejercicios para después del video
3)Simplificar