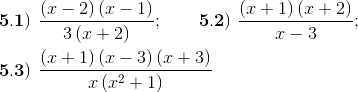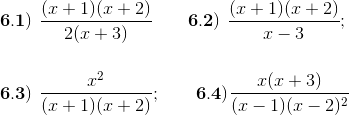EXPRESIONES RACIONALES
VIDEO 1 EXPRESIONES RACIONALES Y FRACCIONES ALGEBRAICAS.
VALORES DE LA VARIABLE QUE HACEN QUE LA EXPRESIÓN NO ESTÉ DEFINIDA.
DOMINIO DE LA EXPRESIÓN
En el video se establece la definición de expresón racional o fracción algebraica. Se muestran ejemplos de expresiones racionales y de expresiones que aún cuando son cocientes no son expresiones racionales. Se discute cuando no está definida y el dominio de una expresión racional. Se muestran ejemplos en que se determina cuando una expresión racional no está definida, pasando luego a determinar su dominio.
Ejercicios
1) Diga cuáles de las siguientes expresiones son racionales
2) Encuentre para qué valores de la variable no está definida cada fracción algebraica o expresión racional
Pulsa el botón para ver las respuestas
VIDEO 2 SIMPLIFICACIÓN DE EXPRESIONES RACIONALES
Se discute cuando la expresión racional está reducida a su mínima expresión o simplificada. Se dan los pasos a considerar para simplificar expresiones racionales: Primero factorizando y luego, cancelando los factores comunes del numerador y del denominador usando el principio fundamental de las fracciones o propiedad de cancelación. Se desarrollan varios ejemplos.
Ejercicios para después del video
3) Simplifique
Pulsa el botón para ver las respuestas
VIDEO 3 EJEMPLO: SIMPLIFICACIÓN
Un ejemplo explica paso a paso cómo obtener la simplificación de una expresión racional. Luego de una primera factorización y cancelación se puede llegar a una expresión racional que puede seguir siendo simplificada. El ejemplo muestra que es necesario considerar la factorización completa de los polinomios del numerador y del denominador para llegar a la mínima expresión. Se pueden ir cancelando los factores comunes que surjan en el proceso de factorización completa. Finalmente, se recomienda escribir los factores no constantes con coeficiente principal igual a uno en la factorización, para conseguir factores comunes.
Ejercicios
4) Simplifique.
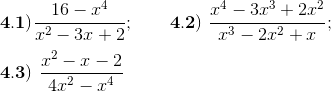
VIDEO 4 MULTIPLICACIÓN DE EXPRESIONES RACIONALES
En el video pasado se justificó cómo determinar el producto de polinomios. En este video daremos ejemplos de cómo multiplicar polinomios en una sola linea. En el video se explica cómo efectuar una multiplicación entre expresiones racionales, mostrando ejemplos en que luego de desarrollar el producto se considera simplificar la expresión.Ejercicios para después del video
3) Multiplique y simplifique:
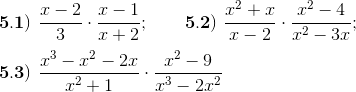
Pulsa el botón para ver las respuestas
VIDEO 5 DIVISIÓN DE EXPRESIONES RACIONALES
En el video se explica cómo efectuar división entre expresiones racionales, mostrando ejemplos en que luego de efectuar la división se considera simplificar la expresión. Cuando la división viene indicada por medio de una fracción se puede efectúar por la ley de extremos y medios.Ejercicios para después del video
6) Efectúe y simplifique
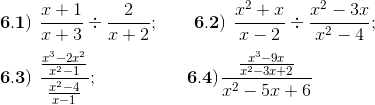
Pulsa el botón para ver las respuestas
OTRO VIDEO DE MULTIPLICACIÓN DE EXPRESIONES RACIONALES

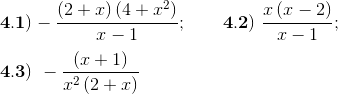 Las expresiones 4.1 son iguales salvo en $x=2,$ donde la original no está definida y la simplificada si.
$ x=1$ no está en el dominio de las dos expresiones.
Las expresiones 4.1 son iguales salvo en $x=2,$ donde la original no está definida y la simplificada si.
$ x=1$ no está en el dominio de las dos expresiones.