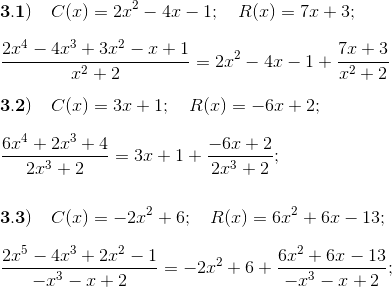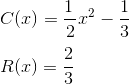DIVISIÓN DE POLINOMIOS

VIDEO 1
DIVISIÓN DE POLINOMIOS

Se explica la división larga entre polinomios, comparándola con la división de los números enteros. Se muestra un ejemplo de cómo se efectúa la división, Luego, se expresa el dividendo en términos del cociente, residuo y divisor.


Ejercicios Efectúe las divisiones dadas.
Exprese el dividendo en términos del cociente, residuo y divisor.

a) $(x^5+3x^4-2x^3-4x^2-x+4)\div (x^3+2x^2-x+2);\qquad$
b) $(2x^4+2x^3-x^2+x+4)\div (x^2+2x+2);$
c) $(-4x^3+2x^2+x+1)\div (2x^2-3x+2);$

Respuestas




   

VIDEO 2
EJERCICIO DE DIVISIÓN DE POLINOMIO

Intenta hacer la división planteada en el video antes de ver cómo se resuelve.




Ejercicios para después del video
Efectúe las divisiones planteadas.
Exprese el resultado de la división en términos fraccionarios.

3.1) $(2x^4-4x^3+3x^2-x+1)\div (x^2+2); \qquad$
3.2) $(4+2x^3+6x^4) \div (2x^3+2);\qquad$
3.3) $(2x^5-4x^3+3x^-1)\div (2-x-x^3)$


Pulsa el botón para ver las respuestas






   

ANIMACIÓN
DIVISIÓN DE POLINOMIOS CON COEFICIENTES FRACCIONARIOS

Se encuentra el residuo y el cociente de una división donde los coeficientes son fracciones.


Ejercicios
Encuentre el cociente y el resto de la división planteada.

Pulsa el botón para ver las respuestas




   

DIVISIÓN ENTRE UN MONOMIO

Cuando el divisor es un monomio, la división se puede realizar por un procedimiento corto. Las ideas de este procedimiento se usan en Cálculo y otras áreas de las Matemáticas para expresar el cociente de un polinomio entre un monomio como una suma de términos de la forma $$ a_rx^r+... a_2x^2+a_1x+a_0,$$ con $r$ un número entero no negativo, pudiendose extender las ideas para no polinomios, con $r$ un número racional.

El video describe mediante ejemplos los dos procedimientos.


Ejercicios
4.1) Efectúe las siguientes divisiones por el procedimiento descrito en el video. Puntualice el cociente y el residuo.
a) $ 2x^4- 6x^3 + 3x^2 – 2x + 1 \div x^2; $
b) $ 6x^5 – x^3 + 3x^2 + 4 \div 3x^3$

Recuerde expresar la división en forma fraccionaria. Luego, descomponer como una suma de fracciones con denominadores iguales al divisor. En cada una de las primeras fracciones está cada término del numerador con grado mayor que el denominador. En estas fracciones simplifique. El numerador de la última fracción contiene los términos del dividendo con grado menor que el grado del divisor, el numerador es el resto o residuo de la división.

4.2) Exprese cada una de las expresiones racionales dadas como una suma de términos de la forma $ a_rx^r$ con $r$ un número racional.
a) $\dfrac{6x^5-2x^2}{2x^2};$
b) $\dfrac {6x^{7/3}-5x^2-8}{2x^2}$

Pulsa el botón para ver las respuestas

4.1)
a) $C(x) = 2x^2 – 6x + 3 ; $ $\qquad R(x)= –2x + 1;$
b) $ C(x) = 2x^2 –1/ 3 ; $ $ \qquad R(x)= 3x^2 + 4 $

4.2)
a) $ 3x^3 –3/2$
b) $3x^{1/3} – 5/2 – 4x^{–2}$
Hay otras divisiones sintéticas para casos especiales. Mira División sintética de polinomios.
Regla de Ruffini