2.4 Suma de términos con radicales y
racionalización de denominadores
Video 1 SUMA DE RADICALES. RADICALES SEMEJANTES
Se muestra como una expresión que es una suma de términos con radicales se puede simplificar. En el proceso es clave los conceptos de radicales semejantes y simplificación de un radical
Ejercicios para después del video
1) ¿Cuál es la propiedad que permite justificar la suma de radicales semejantes? 2) ¿Cuáles de las siguientes expresiones se pueden reducir a menos términos? Justifique. En caso que se pueda reducir, hágalo.
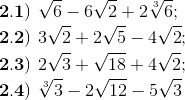
Pulsa el botón para ver las respuestas
↓La propiedad distributiva
2.1) No se puede;
2.2) No se puede
2.3) Luego de simplificar el segundo término $2\sqrt{3}+7\sqrt{2}$
2.4) Luego de simplificar el segundo término $\sqrt[3]{3}+9\sqrt{3}$
VIDEO 2 RACIONALIZACION DE DENOMINADORES. CASO MONOMIO
Existe la convención de expresar las respuestas con el denominador racionalizado. También la racionalización se requiere en otros procesos. En el video se da la definición y se muestran procedimientos para llevar a cabo la racionalización en el caso que el denominador sea un monomio.
Ejercicios para después del video
3) Racionalice el denominador en cada expresión
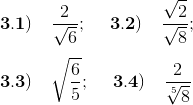
↓
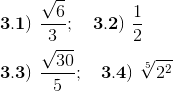
VIDEO 3 SUMA DE TÉRMINOS QUE CONTIENEN RADICALES II
Se continúa sumando términos que contienen radicales. Con la ayuda de la racionalización de denominadores surgirán radicales semejantes que permitirán simplificar la expresión.
Ejercicios para después del video
4) Simplifique cada expresión, reduciendo radicales semejantes
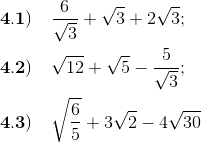
↓
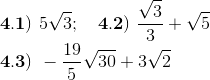
ANIMACIÓN RACIONALIZAR DENOMINADORES. CASO BINOMIO CON RAÍCES CUADRADAS
Se muestra cómo racionalizar el denominador en el caso que el mismo tiene dos términos que contienen solo raíces cuadradas. Se define la conjugada del binomio (radical conjugado)
Ejercicios
5) Racionalice el denominador en cada expresión
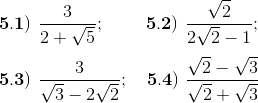
↓

Otros caso CASO TRINOMIO CON RAÍCES CUADRADAS
En el caso que se tenga tres término se aplica la propiedad asociativa para interpretar el denominador como dos términos y poder usar la técnica de la conjugada para racionalizar el denominador, Al aplicar el producto notable de la suma por la diferencia queda otro radical, así que en este caso, la técnica hay que aplicarla dos veces. En el enlace se muestra cómo racionalizar el denominador en este caso.Ejercicios
6) Racionalice el denominador en cada expresión
6.1) $ \quad \dfrac{2}{3+ \sqrt{2} +\sqrt{5}}; \qquad$ 6.2)$\quad \dfrac{\sqrt{3}}{2\sqrt{2}-\sqrt{3}-1} $
Respuestas
Más del caso trinomio con
raíces cuadradas
CASO BINOMIOS CON RAÍCES CÚBICAS
En el caso que se tienen dos términos en el denominador con raíces cúbicas se usa las factorizaciones de diferencia y de suma de cubos para buscar el factor racionalizante, se aplican de manera análoga al caso de binomios con raíces cuadradas.
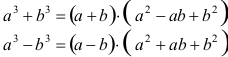
Ejercicios
7) Racionalice el denominador en cada expresión.
7.1) $ \; \dfrac{4}{2 +\sqrt[3]{3}} ; \qquad $ 7.2) $ \; \dfrac{\sqrt[3]{2}}{2\sqrt[3]{2}-1}$
Respuestas
Racionalización de binomios
con raíces cúbicas
