Gráficas de funciones exponenciales
y de funciones que las contienen
Las formas de las gráficas de las funciones exponenciales,
f(x)=bx, dependen
básicamente de la base: si b es mayor a 1 o si
está en (0,1). En principio, obtendremos las gráficas a través de una tabla de valores, pero luego hacemos una descripción de la tabla que
nos ayudará a entender el comportamiento de estas funciones. Graficaremos algunas funciones que contienen
expresiones exponenciales haciendo transformaciones elementales de gráficas de funciones exponenenciales.
Video 1 Definición de la función exponencial Gráfica y características
Se obtendrá la forma de la gráfica de una función exponencial con base $b > 1$, señalando las características más importantes de la funciónPreguntas para después del video a) ¿Cuál es la diferencia significativa entre la gráfica de la función exponencial con base 3 y la de base 5?
Pulsa el botón para ver las respuestas
Video 2 Gráfica y características de la función exponencial con base $b$ entre 0 y 1 ( $0\lt b\lt 1$ )
La gráfica de la función exponencial $f(x)=b^x$ con $ b>1$ ya fue establecida en el video pasado. En base a esta gráfica se puede deducir la gráfica de la función exponencial con base $b$ entre 0 y 1, sin necesidad de una tabla de valores. En base a las informaciones aportadas por la gráfica se señala las características más importante de esta función exponencial.
Gráfica de funciones con expresiones exponenciales usando transformaciones de gráficas elementales
A partir de la gráfica de las funciones exponenciales como función elemental se puede bosquejar la gráfica de otras funciones cuya fórmula se obtiene a partir de operaciones algebraicas de las exponenciales. Para cada función se señala fácilmente las características más importantes a partir de la gráfica como dominio, rango, crecimiento, asíntotas, intersecciones con los ejes. EnTransformaciones de gráficas de funciones.
podrás repasar traslaciones o desplazamientos, contracciones, reflexiones a partir de la gráfica conocida de una función.
Por ejemplo, se puede obtener la gráfica de $y=2^x+2$ a partir de la gráfica de $y=2^x$ por una traslación de 2 unidades hacia arriba.

Cómo determinar las intersecciones con los ejes
Las intersecciones de la gráfica de la función con los ejes son los puntos donde la gráfica corta el eje $x$ y el eje $y$. En algunas ocasiones se pueden obtener a través del gráfico.
Ejemplo La gráfica $y=2^x+2$ claramente no tiene cortes con el eje $x$. Vemos a través del gráfico de $y=2^x+2$ que el corte con el eje $y$ es el punto $(0,3) $
Hay funciones que no se puede obtener la información de manera precisa de los puntos de corte con los ejes por medio del bosquejo de la gráfica. Entonces se intenta de determinar analíticamente.
Determinación analítica de los puntos de intersección con los ejes.
Recuerda
Ejercicios Grafique cada una de las funciones dadas. Señale las características más importantes de cada una. Encuentre intersecciones con lo ejes que no puedan ser encontradas de manera gráfica. $ a) \ f(x)=2^{x-1}; \qquad b) \ g(x)= 2-3^x$ $ c) \ h(x)=2-e^{-x}$
Ejemplo Obtenga la gráfica de $y=2^x-1$. A partir de la gráfica obtenga los cortes.
Ejemplo Determinar la intersección de la gráfica $y=2^{2x+1}+5$ con el eje $y$ y con el eje $x$ de manera analítica.
Ejercicio resuelto Encontrar el punto de intersección de la gráfica de $f(x)=7-3^{x+2}$ con el eje $x$.
Solución
Estimar soluciones de una ecuación exponencial por medio de la gráfica
Suponga se tiene una ecuación equivalente a $f(x)=g(x)$ con $f$ y $g$ funciones con gráficas conocidas. Las soluciones de la ecuación son las $x$ de los puntos de intersección de las dos gráficas.Observe que al plantearnos $f(x)=g(x)$, buscamos los $x_i$ en que los valores de las funciones, $y_i$ coinciden. $(x_i,f(x_i))$ es un punto de la gráfica de $f$ y, como $f(x)=g(x)$, también es un punto de la gráfica de $g$: es un punto de intersección de las dos gráficas.
Si se quiere estimar las soluciones de una ecuación usando gráficas de funciones primero se consigue una ecuación equivalente a la original con la forma $f(x)=g(x)$ con $f$ y $g$ funciones con gráficas conocidas. Luego se estima las coordenas $x$ de los puntos de intersección de las dos gráficas. Éstas son las soluciones. Si las gráficas no se cortan entonces la ecuación no tiene solución. Ejercicio resuelto
Determine el número de soluciones de la ecuación $2^x-3^{-x}+1=0$
Estime gráficamente la(s) solución(es) Solución

 Para $x>0$, la gráfica de $y=5^x$ está por encima de la gráfica de $y=3^x$. En esta zona la gráfica de $ y=5^x$ crece más rápido que la gráfica de $y=3^x$
.
En cambio, para $x\lt 0$, la gráfica de $y=5^x$ está por debajo de la gráfica de $y=3^x$. En el segundo cuadrante la gráfica de $y=5^x$ se pega más rápidamente al eje $x$
Las gráficas se intersecan en $(0,1)$
Para $x>0$, la gráfica de $y=5^x$ está por encima de la gráfica de $y=3^x$. En esta zona la gráfica de $ y=5^x$ crece más rápido que la gráfica de $y=3^x$
.
En cambio, para $x\lt 0$, la gráfica de $y=5^x$ está por debajo de la gráfica de $y=3^x$. En el segundo cuadrante la gráfica de $y=5^x$ se pega más rápidamente al eje $x$
Las gráficas se intersecan en $(0,1)$
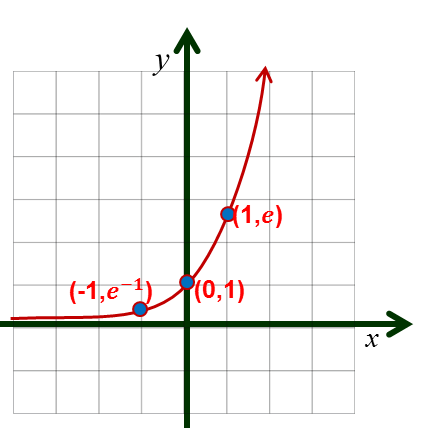 Como la base $e$, 2,71..., es mayor que 1, la gráfica tiene la misma forma a las dadas.
Una pequeña tabla de valores permite precisar un poco más la gráfica $y=e^x$
\begin{array}{|c|c|}
\hline
x & y \\
\hline
-1 & e^{-1} \\
0 & 1 \\
1 & e \\
\hline
\end{array}
$e^{-1} \approx 0,37...$
Como la base $e$, 2,71..., es mayor que 1, la gráfica tiene la misma forma a las dadas.
Una pequeña tabla de valores permite precisar un poco más la gráfica $y=e^x$
\begin{array}{|c|c|}
\hline
x & y \\
\hline
-1 & e^{-1} \\
0 & 1 \\
1 & e \\
\hline
\end{array}
$e^{-1} \approx 0,37...$
 Informaciones:
1) Dom$=R$;
Rango$=(0,\infty)$
2) Es creciente.
3) Corta el eje $y$ en $(0,\frac{1 } {2 })$
No corta el eje $x$
4) La recta $y=0$ (Eje $x$) es una asíntota horizontal por la izquierda.
5) La función en biunívoca
(uno a uno).
Informaciones:
1) Dom$=R$;
Rango$=(0,\infty)$
2) Es creciente.
3) Corta el eje $y$ en $(0,\frac{1 } {2 })$
No corta el eje $x$
4) La recta $y=0$ (Eje $x$) es una asíntota horizontal por la izquierda.
5) La función en biunívoca
(uno a uno).
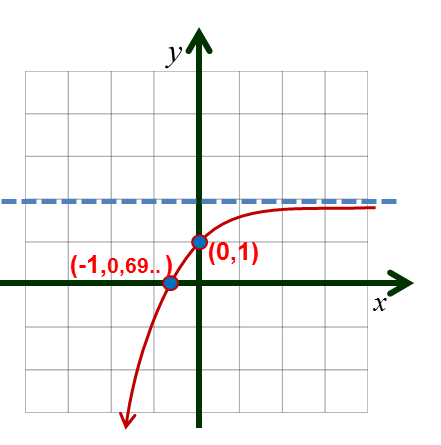
 Informaciones:
1) Dom$=R$;
Rango$=(-\infty,2)$
2) Es decreciente.
3) Corta el eje $y$ en $(0,1)$
Corta el eje $x$ en $(0,\frac{\ln 2 } {\ln 3 })$
4) La recta $y=2$ es una asíntota horizontal por la izquierda.
5) La función en biunívoca
(uno a uno)
Informaciones:
1) Dom$=R$;
Rango$=(-\infty,2)$
2) Es decreciente.
3) Corta el eje $y$ en $(0,1)$
Corta el eje $x$ en $(0,\frac{\ln 2 } {\ln 3 })$
4) La recta $y=2$ es una asíntota horizontal por la izquierda.
5) La función en biunívoca
(uno a uno)