Funciones logarítmicas

Definiremos la función logarítmica como la inversa de la función exponencial, esto nos permitirá deducir muchas propiedades de los logaritmos. Estudiaremos los logaritmos naturales y decimales, cómo leer y cómo determinar logaritmos usando la definición, pasando de la forma logarítmica a la exponencial.

Contenido
1 Definición de la función logarítmica. Partes de un logaritmo 2 Logaritmos naturales y decimales 3 Cómo determinar logaritmo por definición 4 Cómo leer expresiones con logaritmos

Video 1
Definición de la función logarítmica


Se define la función logarítmica como la inversa de la función exponencial, estableciendo la forma exponencial y logarítmica como proposiciones equivalentes. Se realizan ejercicios para pasar de una forma a otra.


Ejercicios para después del video
Pasar las formas exponenciales a logarítmicas. Pasar las formas logarítmicas a exponenciales
a) $2^3 = 8;$
b) $\log_{0,5} (4) = –2;$
c) $\log_2 (16) = 4$
Respuestas
a) $\log_ 2(8) = 3; $
b) $(0,5)^{-2} = 4;$
c) $2^4 = 16$






   




   


Video 2
Logaritmos naturales y decimales

En el siguiente video se definen los logaritmos naturales y decimales. Se sigue con ejercicios sobre pasar de una forma a la otra. Además comenta el uso de los paréntesis para delimitar el argumento de los logaritmos y se enseña el uso de la calculadora para determinar logarítmos.


Ejemplo 1) Indique en cada expresión el argumento del logaritmo Escriba paréntesis para delimitar cada argumento.
a) $\log x+1;\quad$
b) $\log x^2;\quad $
c) $(\log x)^2$
Se aplica la fórmula de cambio de variable al logaritmo en base 4
a) Argumento = $x;\qquad \log(x)+1;$
b) Argumento = $x^2;\qquad \log(x^2);$
a) Argumento = $x;\qquad (\log(x))^2;$





   

Cómo determinar logaritmos por definición

Hay logaritmos en que no es posible determinarlos por cálculos sencillos. Hay otros en que se puede encontrar su valor aplicando la definición.
Nosotros hemos definido la función logarítmica como la inversa de la función exponencial. Así que los pasos para determinar algunos logaritmos son
⋄ Definir y igual al logaritmo a deteminar. (Recordar que el logaritmo es el exponente de la forma exponencial)
⋄ Luego pasar a la forma exponencial y de allí tantear el exponente que es el logaritmo.

Ejercicio resuelto Determine $\log_3 (81)$ usando la definición
Solución explicada paso a paso




Ejercicios
Determine el logaritmo sin usar calculadora

a) 3;  b) –3;  c) –2




   


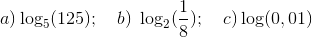
Cómo leer expresiones con logaritmos


En ocasiones se tienen expresiones con logaritmos que se quiere expresar en palabras, de manera verbal. Las ideas clave para traducirlas son decir primero lo que es la expresión: si un logaritmo, un producto, una suma, etc. Cuando se vaya a expresar la parte con logaritmo, identificar el argumento, para entonces decir que es el logaritmo de una suma o un producto o de lo que corresponda.


Ejemplo La expresión $x\log (\sqrt{x})$ la podemos leer como el producto de $x$ por el logaritmo decimal de la raíz de $x$.

Ejercicios
Exprese de manera verbal las siguientes expresiones


a) El logaritmo decimal de la suma del cuadrado de $x$ con 3;
b) La suma de logaritmo decimal del cuadrado de $x$ con 3;
c) El logaritmo decimal de la raíz de $x$;
d) La raíz del logaritmo decimal de $x$.