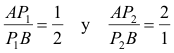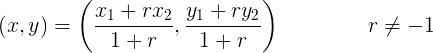División de un segmento de recta en una razón dada
Animación
Punto P que divide un segmento en una razón dada
Sin fórmula
En la animación tienes un ejemplo que muestra cómo encontrar las coordenadas de un punto P que divide al segmento AB en una razón r dada, sin usar una fómula, tan solo valiendonos de resultados sobre triángulos semejantes.
Recuerda que
1) Si en dos triángulos verificamos que dos pares de ángulos
son congruentes entonces los triángulos son semejantes.
Es decir, si podemos comprobar que las medidas de dos
ángulos de un triángulo son iguales a dos de los ángulos del
otro triángulo entonces los triángulos son semejantes. (No hace
falta verificar la tercera correspondencia, ¿por qué?)
2) Si los triángulos son semejantes entonces las razones entre
los lados correspondientes son iguales.
Ejercicios para después de la animación
1) Obtenga las coordenadas del punto P que divide al segmento cuyos extremos son A(-2,-4) y B(1,4) en la razón AP/PB=1/6.
2) Hallar las coordenadas del punto P que divide el segmento AB en la razón AP/PB=2, donde A(1,2) y B(4,5). (Escriba la razón r como 2/1)
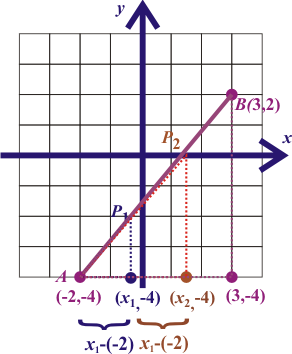
3) Dados los puntos A(-5,-4) y B(-1,2), determine el punto P1 que divide el segmento de recta AB en la razón AP1/P1B=1/2, encontrar el punto P2 que divide ese mismo segmento en la razón AP2/P2B=2.
En el ejercicio 3) se está determinando los puntos P1(x1,y1) y P2(x2,y2) que dividen el segmento AB en tres partes iguales. Podemos ser más eficientes, al darnos cuenta que el segmento de A a (x1,-1), tiene la misma longitud que el segmento de (x1,-1) a (x2,-1), dada por x1-(-5), donde -5 es la coordenada x del punto A.(De nuevo, puede ser demostrado por semejanza de triángulos). Entonces x2 lo determinamos a partir de la coordenada x1
x2=x1+(x1-(-5))
Igual consideración podemos hacer con las coordenadas y de los puntos P1 y P2.
Puedes investigar más en el enlace.
4) Dados los puntos A(1,-5) y B(8,3), encontrar los puntos que dividen el segmento de recta AB en cinco partes iguales.
Podemos demostrar una fórmula general para el problema.
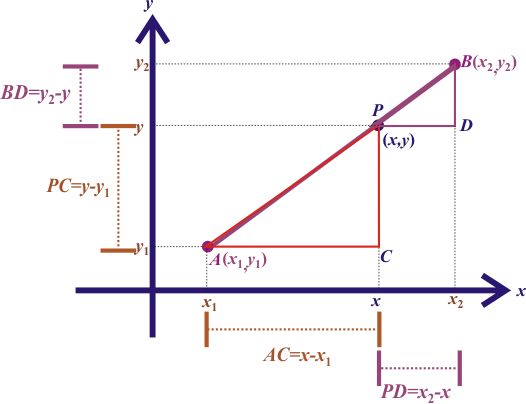
Ejercicios
5) Apóyese en la figura y en las ideas expuestas en la animación para deducir la fórmula.
6) Verifique la fórmula, empleándola para resolver el ejercicio 1.
7) El segmento AB está dividido por el punto P(2,1) en una razón de 1/6, esto es AP/PB=1/6. Si B(3,4), determine las coordenadas del punto A.
En el documento tienes las respuestas a los primeros problemas planteados y los últimos ejercicios resueltos.