LA PENDIENTE
CONCEPTOS
Se explica el concepto de pendiente de una recta. Antes de establecer formalmente la definición de la pendiente, se hacen comentarios provechosos, que permiten ver la consistencia de la definición.

Elevación entre recorrido como una medida de la inclinación de una recta
LA PENDIENTE
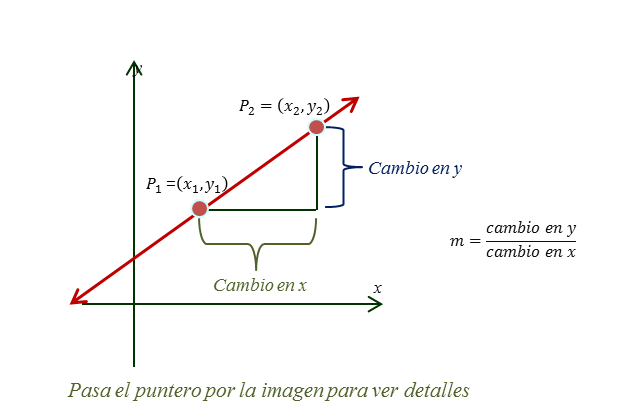
La pendiente de una recta no vertical es una medida de la inclinación de la recta, dada como la razón entre la elevación y el recorrido y denotada por la letra m.
Si la recta está ubicada en el plano cartesiano es posible determinar la pendiente de la recta a través de cualesquiera dos puntos distintos de la recta, $P(x_1,y_1),P(x_2,y_2)$. La elevación correspondería al cambio en $y$ y el recorrido al cambio en $x$. $$ m=\frac{\text{cambio en }y}{\text{cambio en } y}=\frac{\Delta y}{\Delta x}$$
Podemos expresar la pendiente en términos de las coordenadas de los puntos,
$$ m=\frac{y_2-y_1}{x_2-x_1}$$
Observe que no tiene sentido aplicar la fórmula cuando $x$ no cambia. Esto ocurre sólo en rectas verticales. Las rectas verticales no tienen pendientes definidas. En los videos de esta página estaremos insistiendo en este concepto y otras ideas.
Esta medida de inclinación se asemeja a nuestro concepto intuitivo de pendiente, cuando hablamos de la pendiente de una rampa, de una montaña. A mayor pendiente, en valor absoluto, mayor inclinación de la recta.

Rectas que descienden (de izquierda a derecha) tienen pendientes negativas.

Ejemplo Calcule la pendiente de la recta que pasa por los puntos (2,–3 ) y (–1 ,5)
Con las coordenadas de dos puntos podemos determinar la pendiente de la recta.
Pendientes 0 corresponden a rectas horizontales.
Pendiente positiva si y sólo si la recta sube (de izquierda a derecha).
Pendientes negativas corresponden a rectas de descienden.
Las rectas verticales no tienen pendientes definidas.
LA PENDIENTE. CONCEPTOS
Se explica el concepto de pendiente de una recta. Antes de establecer formalmente la definición de la pendiente, se hacen comentarios provechosos, que permiten ver la consistencia de la definición.
EJEMPLO DE CÁLCULO DE LA PENDIENTE
Video elemental. Se muestra cómo encontrar la pendiente de la recta dado dos puntos sobre la misma, mediante dos ejemplos.
Ejercicio para después del video
Encuentre la pendiente de la recta que pasa por los puntos dados en cada caso.
a) (-1,0) y (2,6); b) (3,-5) y (4,-6);
c) (0,4) y (-4,-2)
GRAFICAR UNA RECTA DADO UN PUNTO Y LA PENDIENTE
Se muestran dos ejemplos de cómo trazar la recta dado un punto de la misma y el valor numérico de la pendiente.
Ejercicio para después del video
Grafique cada recta con las informaciones dadas en cada caso.
a) Pasa por el punto (2,0) y tiene pendiente 2.
b) Pasa por el punto (-3,1) y tiene pendiente 1/3.
c) Pasa por el origen y tiene pendiente -4.
d) Pasa por el punto (1,2) y tiene pendiente -2/3. (Solución en el próximo video).
GRÁFICAR UNA RECTA DADO UN PUNTO Y LA PENDIENTE
Se muestra la resolución del ejercicio d).
Ejercicios para después del video
Grafique la recta con las informaciones dadas.
a) Pasa por el punto (2,-3) y tiene pendiente 4/3.
b) Corta el eje x en 2 y tiene pendiente -4/3.
RECTAS HORIZONTALES Y VERTICALES. PENDIENTE
¿Qué pasa con las pendientes de rectas horizontales?
¿Que puede decir acerca de la pendiente de una recta vertical?
Ejercicio para después del video
Conteste las preguntas de arriba.
ESTIMACIÓN DE LA PENDIENTE DE UNA RECTA
Se estima la pendiente de distintas rectas. Algunas estimaciones se hacen de manera geométrica, otras usando la simetría
Ejercicios para después del video
Estime el valor de la pendiente para cada una de las rectas dadas




