Punto medio de un segmento de recta


Contenido
1 Obtención de las fórmulas de las coordenadas del punto medio 2 Ejemplo 3 Problemas

Video 1
DEMOSTRACIÓN DE LA FÓRMULA DE LAS COORDENADAS DEL PUNTO MEDIO ENTRE DOS PUNTOS

En el video se deduce la fórmula de las coordenadas del punto medio del segmento de recta que une dos puntos con coordenadas conocidas. En la demostración se construyen dos triángulos semejantes, que permiten deducir la fórmula, de manera constructiva.

   

Decimos que

Las coordenadas del punto medio son los promedios de las coordenadas de los puntos extremos






   

Video 2
PUNTO MEDIO ENTRE DOS PUNTOS. EJEMPLO

Se muestra con un ejemplo como hallar las coordenadas del punto medio entre dos puntos usando las fórmulas de las coordenadas del punto medio. Se verifica la respuesta graficando los puntos y el punto medio. También la respuesta es confirmada analíticamente, al demostrar que la distancia entre el punto medio encontrado y cualquiera de los puntos es la mitad de la distancia de los dos puntos.  






   

Ejercicios para después del video
1) Determine las coordenadas del punto medio del segmento de recta con puntos extremos dados
1.1) (1,2) y (-3,4)
1.2) (-3,0) y (-4,6);
1.3) (-1/2,4/3) y (2,3/2)

2) Encuentre las coordenadas del punto medio del segmento de recta que une A(2,-1) y B(4,-3). Muestre que la distancia de A al punto medio es la misma que la distancia de B al punto medio, usando la fórmula de distancia.

3) Las coordenadas de los dos extremos de un diámetro de una circunferencia son (3,6) y (7,8).
3.1) Determine las coordenadas del centro de la circunferencia.
3.2) Determine el radio de la circunferencia.

4) Encuentre el punto P(x,y) tal que (2,3) es el punto medio del segmento de recta que une P con el punto (5,8).
Del hecho que (2,3) es el punto medio del segmento de recta que une (x,y) con (5,8), tenemos

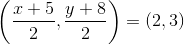Del hecho que las coordenadas deben ser iguales, se plantea y resuelve el sistema de ecuación


5) Usando la fórmula de las coordenadas del punto medio, encuentre las coordenadas del punto que está a tres cuartas partes del camino de A(1,2) a B(3,-2), en el segmento de recta que los une.

Calcular el punto medio entre (1,2) y (3,–2). Es (2,0). El punto buscado está en la mitad del segmento de recta entre (2,0) y (3,–2). Calcular el punto medio entre (2,0) y (3,–2).


El problema 5 puede ser formulado como sigue :Encontrar las coordenadas de un punto que divide al segmento AB en una razón de 3/1. En este caso, se puede resolver aplicando dos veces la fórmula del punto medio, pero no en todos los casos se puede. En el primer enlace puedes ver un procedimiento general.



En el documento en PDF están las respuestas de los ejercicios planteados

Respuestas