3.3 LA CIRCUNFERENCIA
La ecuación
Se deduce la ecuación de la circunferencia, obteniendo la ecuación centro radio, conocida también como la forma canónica o estándar. Con estas dos informaciones se puede conseguir la ecuación de la circunferencia. En la página se desarrolla varios ejemplos en que piden determinar la ecuación de la circunferencia, llevándola a la forma general. Un video muy elemental explica cómo graficar una circunferencia a partir de la ecuación canónica o centro radio. En otro video se presenta la ecuación escrita en su forma general, se lleva a la forma centro radio (canónica) para de allí graficar. La forma de pasarla a la otra forma usa la técnica de completación de cuadrados. Finalmente, se presenta un video en que establece cuando una ecuación con la forma de la ecuación general de una circunferencia es o no la ecuación de una circunferencia.
LA CIRCUNFERENCIA. ECUACIÓN CENTRO RADIO (Canónica)
Se empieza con la definición de una circunferencia, viendo cómo la definición corresponde con la curva. Luego, se establece la ecuación centro radio. Finalmente, se encuentra la ecuación de una circunferencia que cumple con unas condiciones dadas, expresando la respuesta en la forma general.
Ejercicio para después del video Encuentre la ecuación de la circunferencia con centro (-2,3) y radio 5. a) Exprésela en su forma ordinaria (centro-radio o reducida). b) Exprésela en su forma general
ENCONTRAR LA ECUACIÓN DE UNA CIRCUNFERENCIA (Parte I).
El video empieza explicando los problemas en que piden encontrar la ecuación de una circunferencia con unas informaciones dadas, delineando una estrategia general para resolver este tipo de problema. Luego desarrolla un ejemplo.Ejercicio para después del video Para cada uno de los apartados, halle la ecuación de la circunferencia que cumple las condiciones dadas. Escriba su respuesta en la forma ordinaria (centro-radio o reducida) y en la forma general. a) Con centro (-5,1) y pasa por el punto (3,-1) b) Con centro (4,0) y diámetro 6.
ENCONTRAR UNA ECUACIÓN DE UNA CIRCUNFERENCIA (Parte II)
El video empieza explicando los problemas en que piden conseguir la ecuación de una circunferencia con unas informaciones dadas, delineando una estrategia general para resolver este tipo de problema. Se desarrollas dos ejemplos.
Ejercicio para después del video Para cada uno de los apartados, encuentre la ecuación general de la circunferencia que cumple las condiciones dadas. a) Está en el segundo cuadrante, tiene diámetro 6 y es tangente a los dos ejes coordenados. b) Los puntos extremos de un diámetro de la circunferencia son (1,2) y (3,-4).
A PARTIR DE LA ECUACIÓN CENTRO RADIO GRÁFICAR UNA CIRCUNFERENCIA
Video elemental en que explica cómo a partir de la ecuación centro radio (canónica) de una circunferencia se obtiene el centro y el radio de una circunferencia y de allí graficar la ecuación.
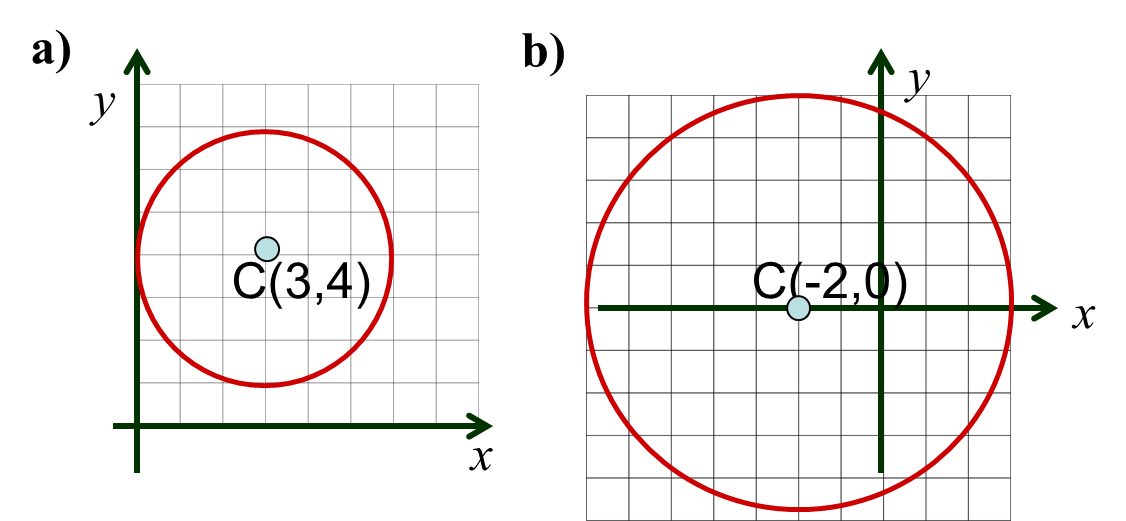
Ejercicios para después del video Obtenga la gráfica de cada una de las siguientes ecuaciones a) $(y-4)^2+(x-3)^2=9$ b) $y^2+(x+2)^2=25$
CENTRO Y RADIO DE UNA CIRCUNFERENCIA A PARTIR DE LA FORMA GENERAL
Se explica cómo llevar una ecuación de una circunferencia escrita en su forma general a su forma centro-radio que permite encontrar el centro y el radio de la misma. Para eso, se usa la técnica de completación de cuadrados. Se desarrolla un ejemplo en que finalmente se obtiene la gráfica de la circunferencia.
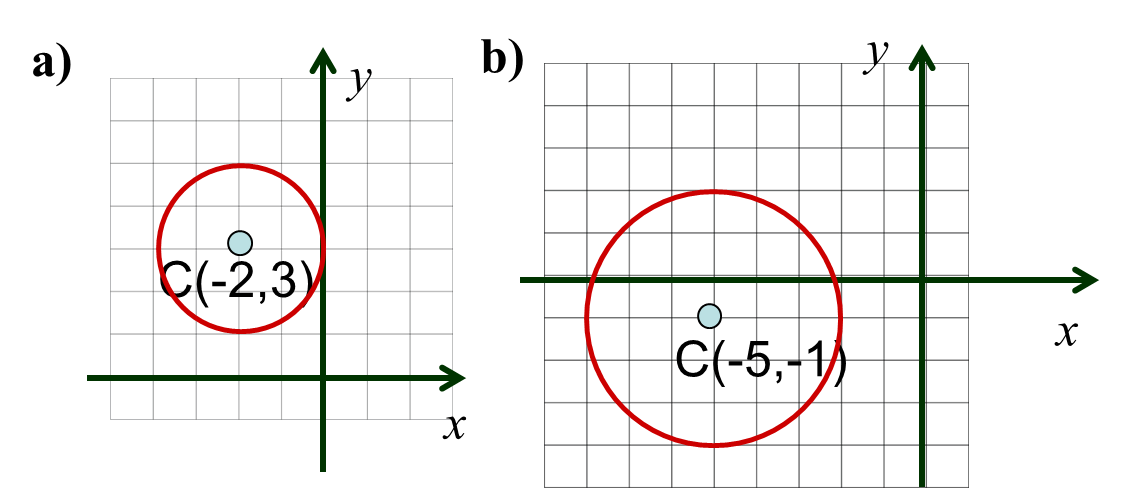
Ejercicios para después del video Determine el centro y el radio de la circunferencia de cada una de las ecuaciones dadas. Grafique la ecuación. a) $x^ 2+y^2+4x-6y+9=0$ b) $y^2+x^2+2y+10x+17=0 $
DETERMINAR SI LA ECUACIÓN ES LA DE UNA CIRCUNFERENCIA
Dada una ecuación con la forma general de una circunferencia se explica las diversas situaciones que se pueden presentar. Se desarrolla un ejemplo.
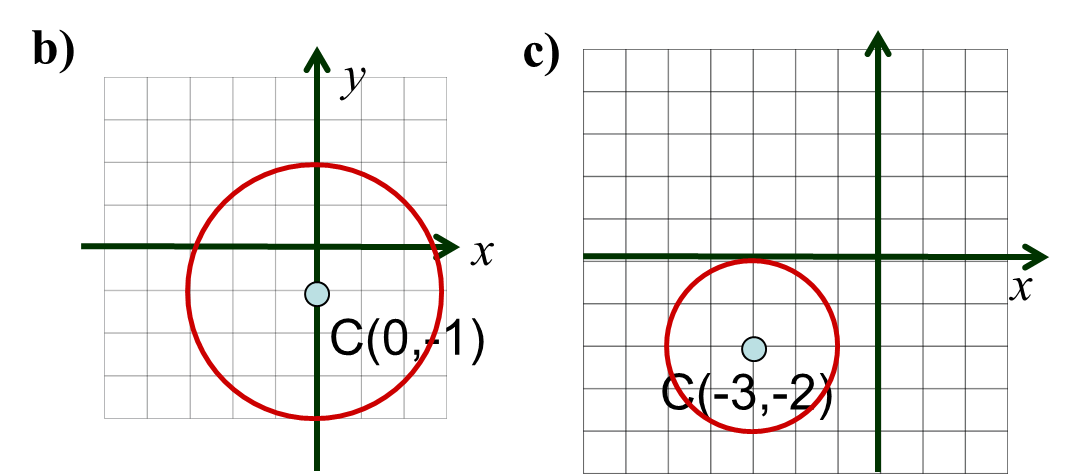
Ejercicios para después del video Para cada una de las ecuaciones dadas determine si corresponede a una circunferencia. En caso que lo sea, determine el centro y el radio y grafique a) $x^2+y^2+4x-6y+16=0 $ b) $ y^2+x^2+2y-8=0 $ c) $ x^2+y^2+6x+4y+9=0 $

 $r=3\qquad\qquad\qquad\qquad$ $r=2$
$r=3\qquad\qquad\qquad\qquad$ $r=2$