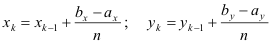Animación

Encuentre las coordenadas del punto que está a dos quintas partes del camino de A(-1,-2) a B(4,2), en el segmento de recta que los une. Definiendo triángulos semejantes adecuados y de la igualdad entre las razones de los lados correspondiente se resuelve el problema planteado.

Ejercicio
1) Determine las coordenadas del punto que está a un sexto del camino de A(-2,3) a B(3,-3). Halle las coordenadas del punto que está a dos sextos del camino de A a B. Si consiguimos el resto de los puntos de la sucesión, los que están a tres sextos, cuatro sextos y cinco sextos del camino que va de A a B, estaremos consiguiendo los punto que dividen el segmento AB en seis partes iguales. Pero, podemos ser eficientes, abajo deducimos fórmulas para encontrar estos puntos.

Recuerda que

1) Si en dos triángulos verificamos que dos pares de ángulos son congruentes entonces los triángulos son semejantes. Es decir, si podemos comprobar que las medidas de dos ángulos de un triángulo son iguales a dos de los ángulos del otro triángulo entonces los triángulos son semejantes. (No hace falta verificar la tercera correspondencia, ¿por qué?)

2) Si los triángulos son semejantes entonces las razones entre los lados correspondientes son iguales.

Cómo encontrar las coordenadas de los puntos que dividen el segmento AB en n partes iguales

Demostración de las fórmulas Sean $A(a_x,a_y)$ y $B(b_x,b_y)$ los puntos extremos de un segmento. En el documento se prueba que las coordenadas de los puntos $P_1, P_2,\cdots P_{n-1}$ que dividen el segmento en n partes iguales pueden ser obtenidas a partir de las longitudes de los segmentos horizontal $AC=b_x-a_x$ y vertical $BC=b_y-a_y$ y de las coordenadas del punto $A$, $(a_x,a_y)$.

Demostración

Ejercicio 2) Demostrar

Ejemplo
Encontrar las coordenadas de los puntos que dividen el segmento con extremos A(-2,1) y B(2,7) en cinco partes iguales.
Solución
Primero encontramos las longitudes de los segmentos proyección de los puntos $A(a_x,a_y)$ y $B(b_x,b_y)$ sobre los ejes.




Determinamos el primer punto

Ahora determinamos los siguientes en base al anterior
Si haces otra iteración encontraras al punto B.



Ejercicio
3) Encontrar las coordenadas de los puntos que dividen el segmento con extremos A(-2,1) y B(2,7) en seis partes iguales

Respuestas y sugerencias