3.8  SISTEMAS DE ECUACIONES Y DESIGUALDADES
LINEALES  EN DOS VARIABLES

SISTEMAS DE ECUACIONES LINEALES EN DOS VARIABLES.
MÉTODO GRÁFICO VS. MÉTODOS ANALÍTICOS.

Se explica el tipo de soluciones de un sistema de ecuaciones lineales con argumentos geométricos. Se establece cómo conseguir las soluciones de un sistema de ecuaciones lineales con dos variables de una manera geométrica, mencionando cuáles son las bondades de este procedimiento. Finalmente, se resuelve un sistema de ecuaciones graficamente y analíticamente

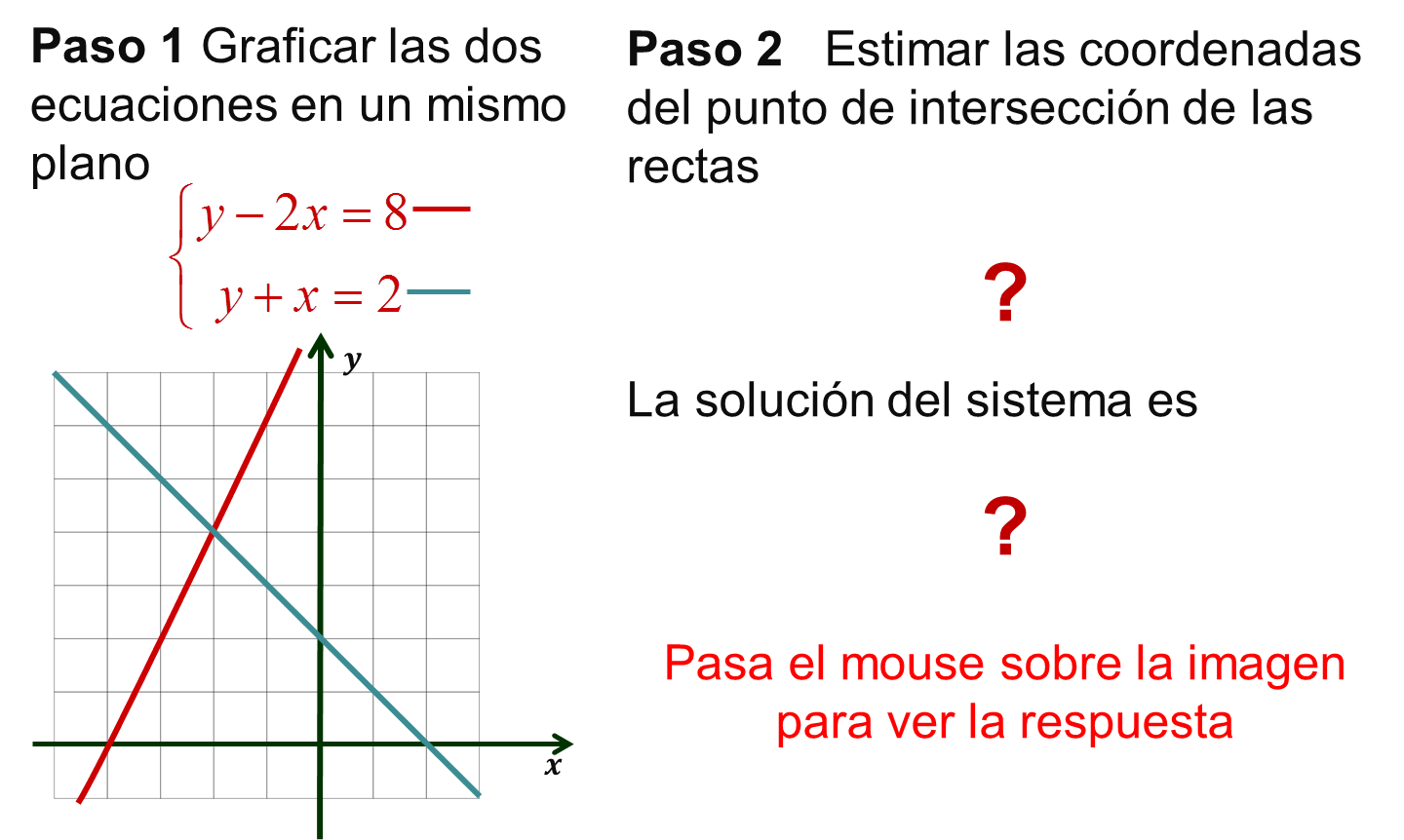
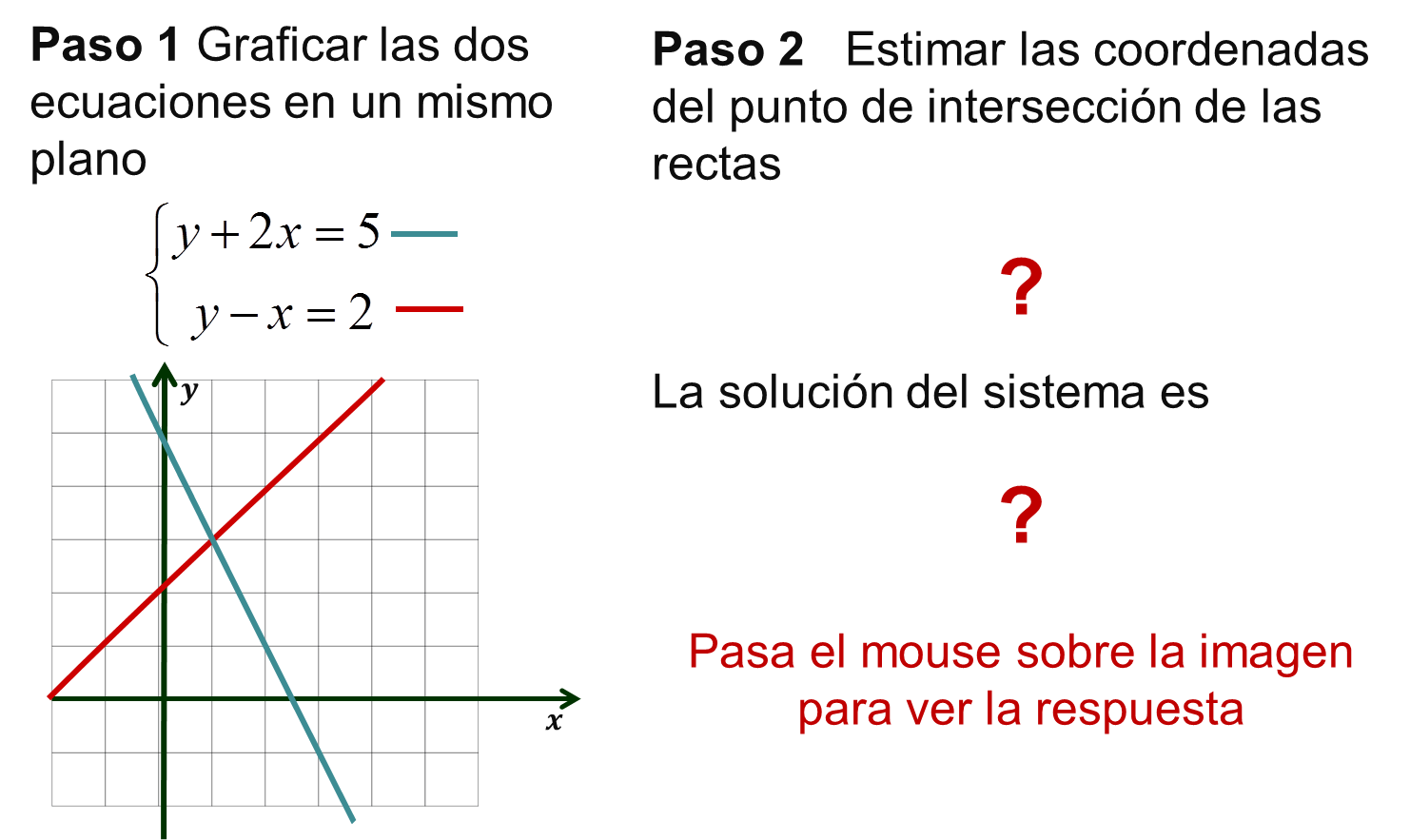
Ejercicios para después del video
Resolver cada uno de los sistemas de ecuaciones dados por el método gráfico.
a) $ \left \{ \begin{array}{rcl} y-2x= 8 \\ y+x= 2\ \end{array} \right . \quad $ b) $ \left \{ \begin{array}{rcl} y+2x=5 \\ y-x =2 \end{array} \right . \quad $
 

---

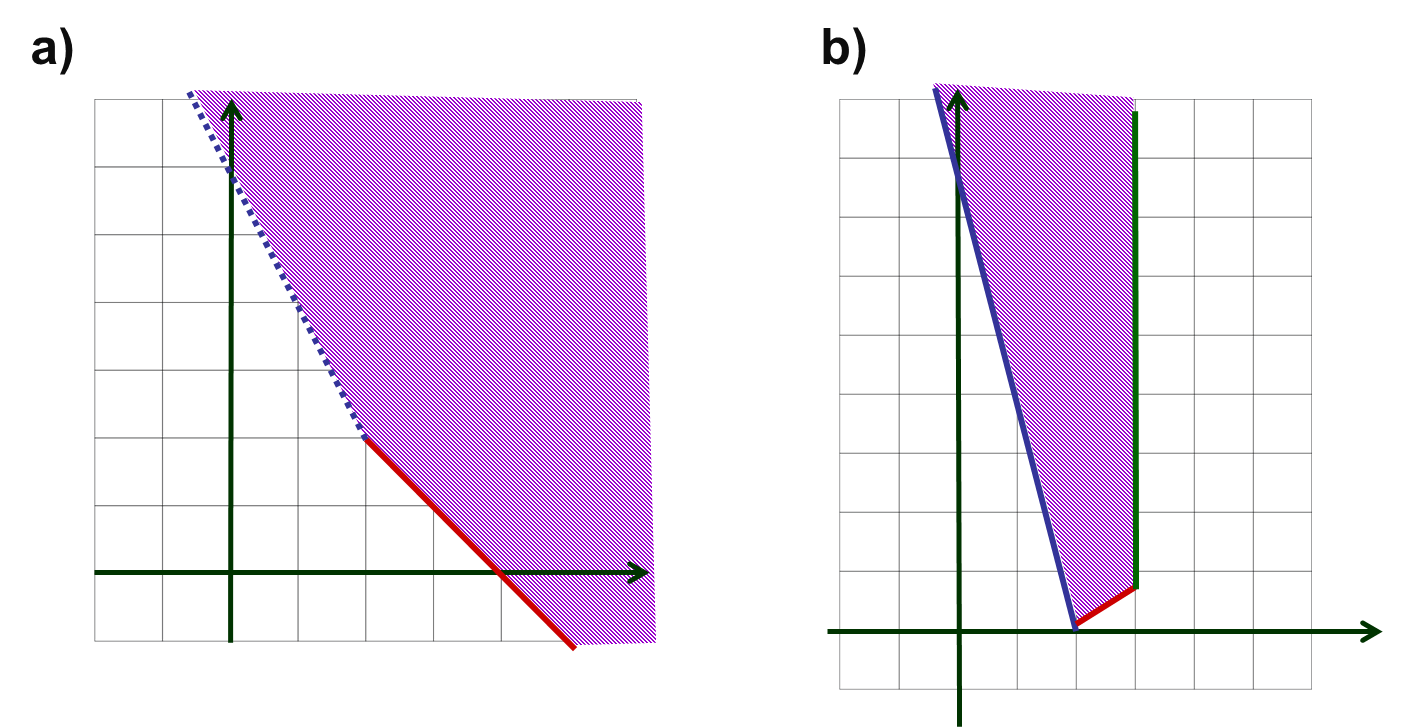
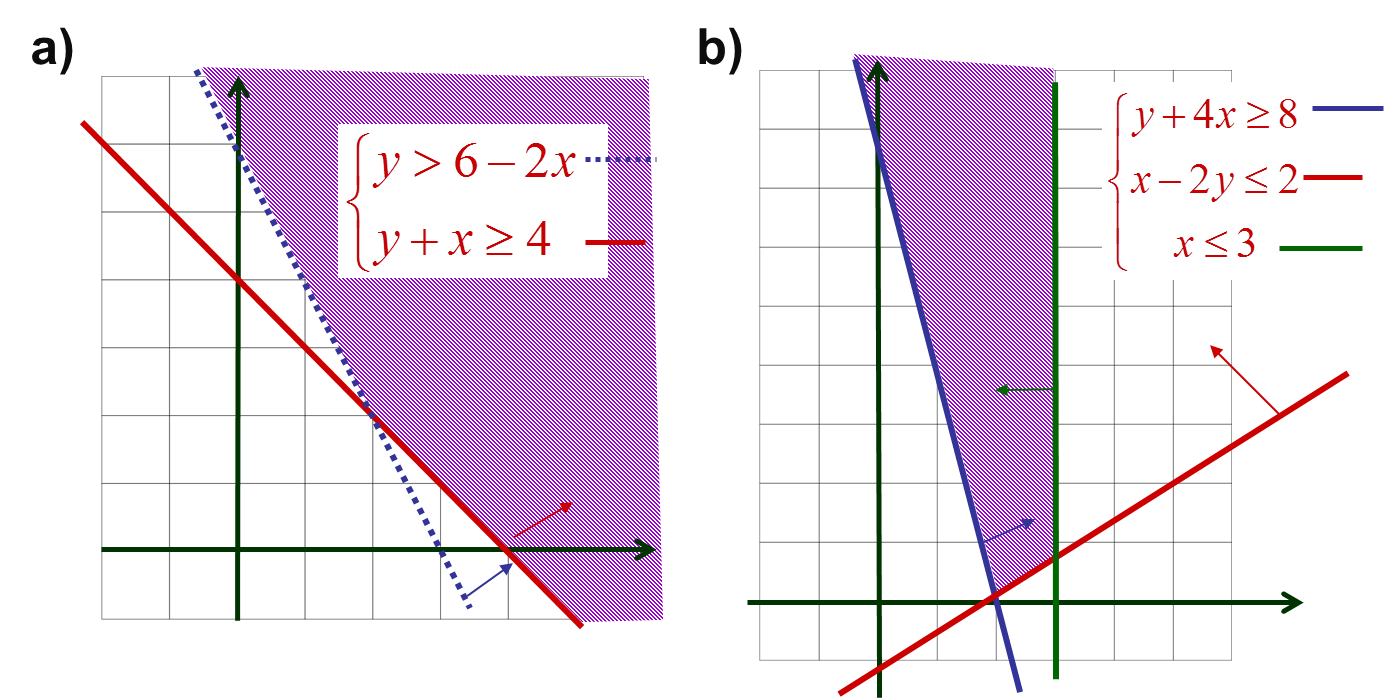
SISTEMAS DE DESIGUALDADES EN DOS VARIABLES. SOLUCIÓN GEOMÉTRICA

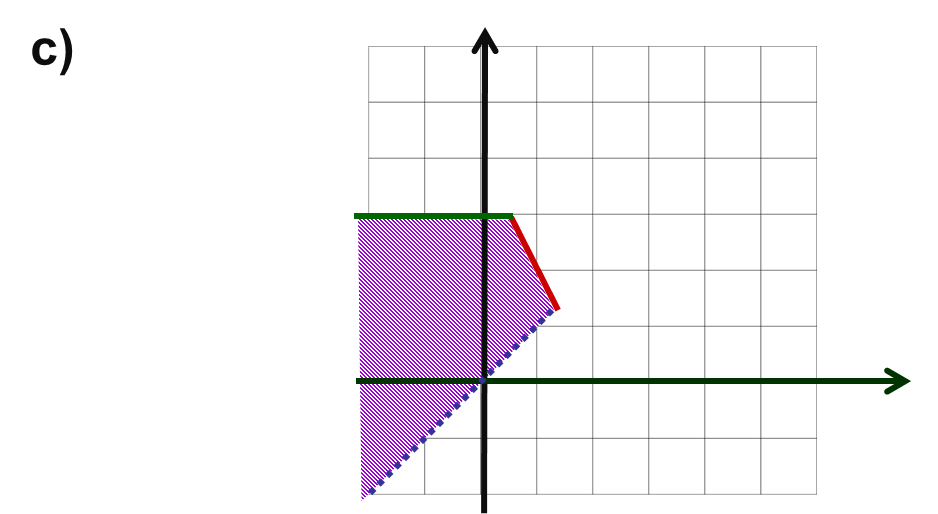
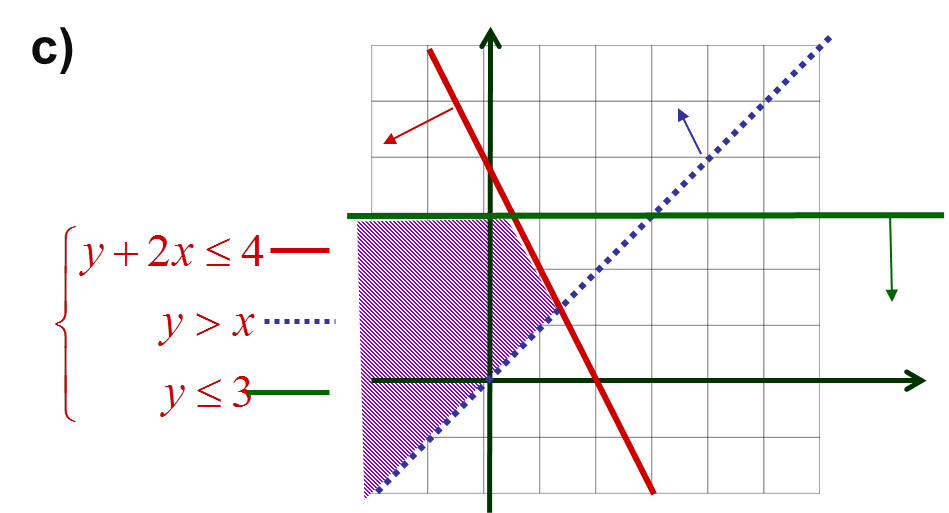
Se dan conceptos claves inherentes a un sistema de desigualdades (inecuaciones).
Se muestra rápidamente una aplicación en que surge un sistema de desigualdades.
Se explica cómo resolver un sistema de inecuaciones con dos incognitas, específicamente un sistema lineal. Finalmente se resuelve de manera gráfica un sistema de desigualdades lineales con dos variables, obteniendo la gráfica del sistema, que no es otra cosa que la gráfica del conjunto solución.

Ejercicio para después del video
Grafique
a) $ \left \{ \begin{array}{rcl} y>6-2x \\ y+x \geq 4 \end{array} \right . \quad $ b) $ \left \{ \begin{array}{rcl} y+4x\leq 8 \\ x-2y \leq 2 \\ x \leq 3 \end{array} \right . \quad $
   

c) $ \left \{ \begin{array}{rcl} y+2x\leq 4 \\ y > x \\ y \leq 3 \end{array} \right . $

---

SISTEMAS DE DESIGUALDADES EN DOS VARIABLES
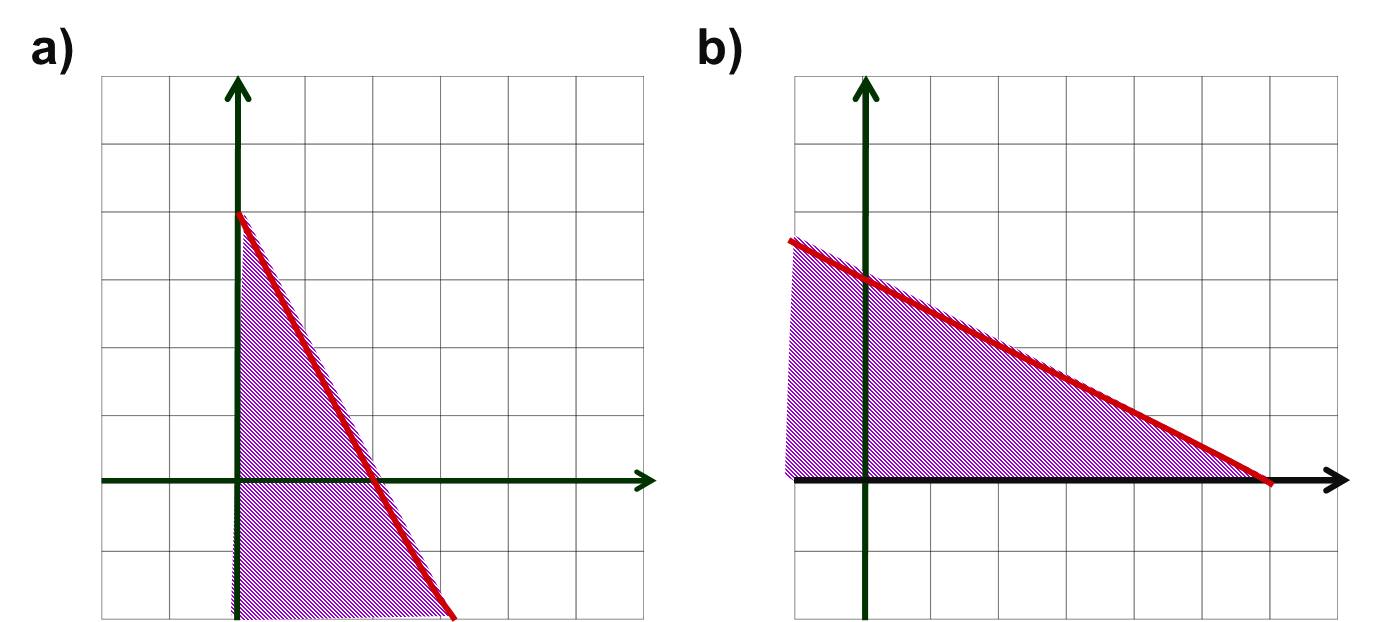
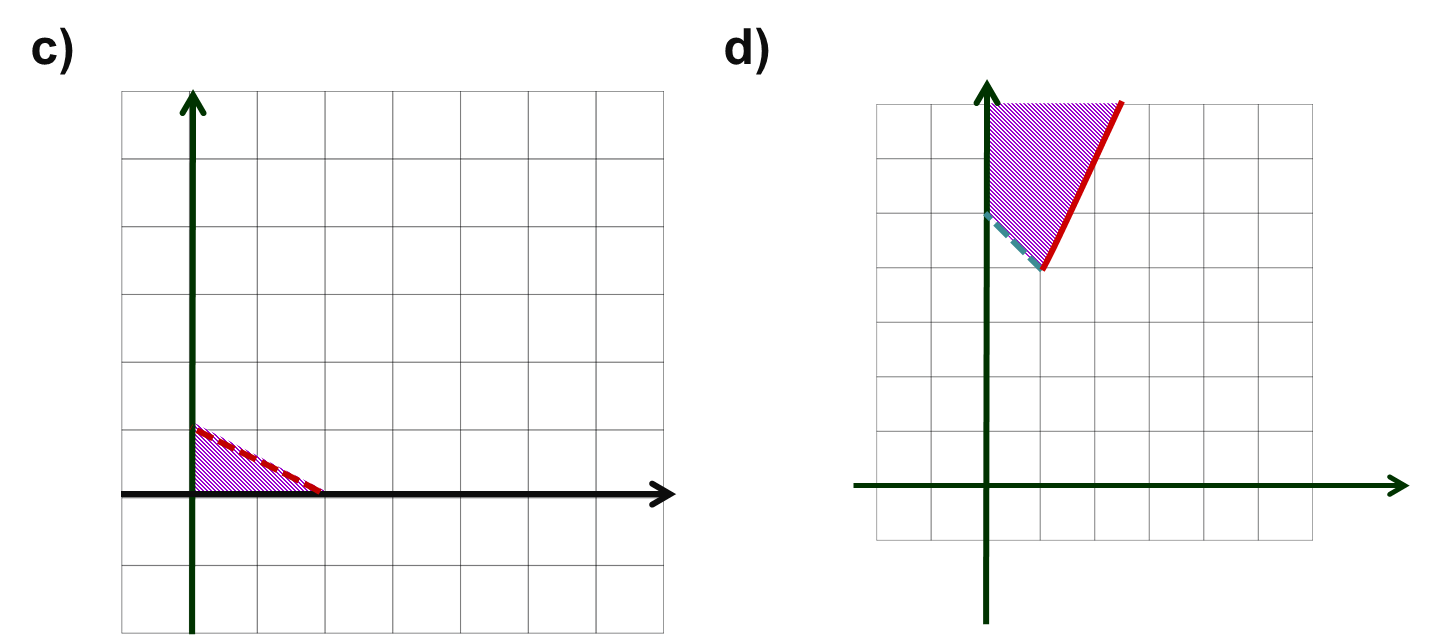
NO NEGATIVAS

Es frecuente en las aplicaciones que surjan sistemas de inecuaciones en que las dos variables sean no negativas. En el documento en pdf exponemos cómo resolver este tipo de sistemas, mostrando dos ejemplos.

Dos ejemplos resueltos

Ejercicios para después del video
Grafique cada uno de los sistemas de desigualdades dados abajo
a) $ \left \{ \begin{array}{rcl} y+2x\leq 4 \\ x \geq 0 \\ \end{array} \right . \quad \quad $ b) $ \left \{ \begin{array}{rcl} 2 y+x\leq 6 \\ y \geq 0 \\ \end{array} \right . $

c) $ \left \{ \begin{array}{rcl} 2 y+x \lt 2 \\ x \geq 0 \\ y \geq 0 \\ \end{array} \right . \quad \quad $ d) $ \left \{ \begin{array}{rcl} y-2x\geq 2 \\ y+x>5 \\ x \geq 0 \\ y \geq 0 \\ \end{array} \right . $