3.5 LA RECTA
Algunas formas de la ecuación
Se explica el concepto de pendiente de una recta. Antes de establecer formalmente la definición de la pendiente, se hacen comentarios provechosos, que permiten ver la consistencia de la definición.
FORMA PUNTO PENDIENTE DE LA ECUACIÓN DE LA RECTA
En el video se deduce la ecuación la recta que pasa por un punto $P(x,y) $ y tiene pendiente igual a $m$. La demostración usa el hecho que la pendiente es invariante sobre cualesquiera dos puntos que se tomen de la recta para calcularla. Se desarrolla un ejemplo en que piden encontrar la ecuación de la recta que pasa por un punto dado y con pendiente conocida. En el ejemplo se explica cómo determinar un punto de la recta conociendo una de sus coordenadas.
Ejercicios para después del video 1 a) Hallar la ecuación de la recta con pendiente -3 y que pasa por el punto $(3,-2)$ ; b) Determine el punto de la recta que tiene coordenada y igual a $-5.$ 2 a) Encuentre la ecuación de la recta con pendiente $ -4$ y que pasa por el origen ; b) Determine el punto de la recta que tiene coordenada $x$ igual a $2.$
ENCONTRAR LA ECUACIÓN DE LA RECTA DADOS DOS PUNTOS DE LA MISMA
Se desarrolla un ejemplo en que pide determinar la ecuación de la recta conociendo las coordenadas de dos puntos de la misma. En el ejemplo también se muestra cómo verificar si un punto está o no sobre la recta de manera analítica.
Ejercicio para después del video 1 a) Consiga la ecuación de la recta con pendiente 5 y que corta el eje $y$ en -5. b) Determine si el punto (-2,3) está o no sobre la recta con un procedimiento analítico. 2 a) Consiga la ecuación de la recta que pasa por los puntos (3,5) y (5,1) ; b) Compruebe si el punto (6,-1) está o no sobre la recta con un procedimiento analítico.
LAS ECUACIONES DE RECTAS HORIZONTALES Y VERTICALES
Se encuentra la ecuación de una recta horizontal usando la forma punto pendiente. Se analiza la ecuación encontrada, interpretando la ecuación como una condición que cumple todos los puntos y sólo los puntos de la recta. A partir de este análisis se establece la condición de una recta vertical y de allí su ecuación.
Ejercicios para después del video Encuentre la ecuación de la recta que satisface las condiciones dadas para cada caso. 1) Es paralela al eje $y$ y pasa por el punto (6,1); 2) Es horizontal y pasa por el punto (3,-4); 3) Pasa por el punto (4,-5) y es vertical.
FORMA GENERAL Y FORMA PENDIENTE ORDENADA AL ORIGEN
Otras formas de la ecuación de la recta son presentadas. Se examina las ventajas de cada una de las formas principales: punto-pendiente, ordenada al origen y la forma general. Se desarrolla un ejemplo en que piden determinar la pendiente de una recta dada su ecuación.
Ejercicio para después del video 1) Haga un cuadro sinóptico en que detalle cada forma, su nombre, su expresión general, los elementos que la constituyen, ventajas o para qué se usa.
2) Encuentre la pendiente y la ordenada al origen de cada recta. a) $ y+3x=4;$ b) $ 2y=5x-5;$ c) $ y-4=0; $ d) $4x-5y= 20$
GRAFICANDO RECTAS A PARTIR DE SU ECUACIÓN
Se muestra los distintos procedimientos para graficar rectas a partir de su ecuación.
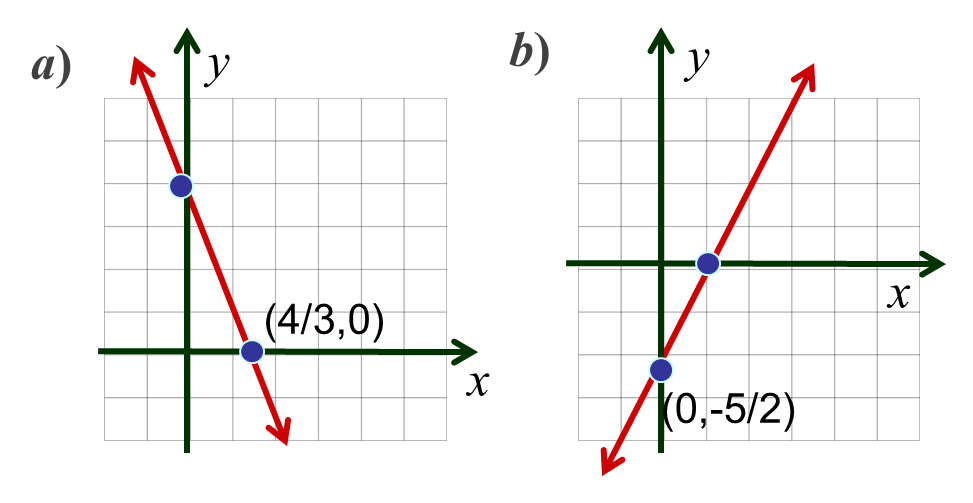
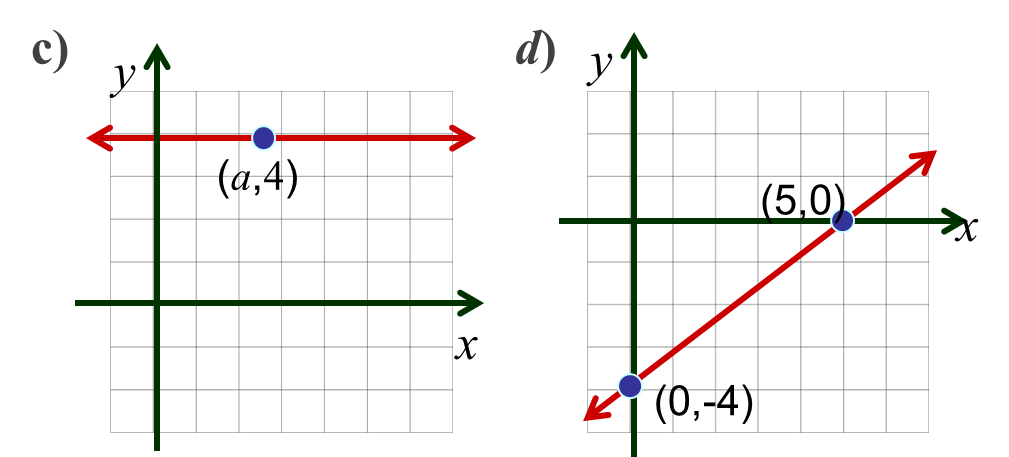
Ejercicio para después del video Grafique las siguientes ecuaciones a) $ y+3x=4; $ b) $ 2y=5x-5; $ c) $y-4=0; $ d) $4x-5y= 20 $