Límites de formas indeterminadas del tipo 0/0
Caso binomio con raíces cúbicas
El límite
Entre las características de la función que se le está tomando
límite tenemos que
Una recomendación para resolver la indeterminación y poder evaluar el límite consiste en
Recuerda que racionalizar el numerador es encontrar una expresión equivalente sin radicales en el mismo.
En límites indeterminados con numerador o denominador binomios con raíces cuadradas se usa la conjugada como el factor racionalizante, pues provoca el resultado de una diferencia de cuadrados. En el caso de raíces cúbicas se busca otro factor racionalizante que al aplicarlo, en el denominador quede una suma o diferencia de cubos, para poder simplificar las raíces del numerador o denominador
Entre las características de la función que se le está tomando
límite tenemos que
- El numerador es un binomio con raíces cúbicas
- El denominador es un polinomio
Una recomendación para resolver la indeterminación y poder evaluar el límite consiste en
- Racionalizar el numerador
- Buscar factores comunes en el numerador y denominador que se anulen en 2
- Cancelar los factores comunes
- Finalmente, si el límite obtenido no es una forma indeterminada pasar a encontrarlo, usando las propiedades de límites
Recuerda que racionalizar el numerador es encontrar una expresión equivalente sin radicales en el mismo.
En límites indeterminados con numerador o denominador binomios con raíces cuadradas se usa la conjugada como el factor racionalizante, pues provoca el resultado de una diferencia de cuadrados. En el caso de raíces cúbicas se busca otro factor racionalizante que al aplicarlo, en el denominador quede una suma o diferencia de cubos, para poder simplificar las raíces del numerador o denominador
Para racionalizar usamos, en el caso que tengamos una diferencia, la siguiente fórmula de diferencia de cubos $$a^3-b^3 = (a-b)( a^2+ab +b^2)$$ En el lado derecho, identificamos $(a-b)$ como la expresión del miembro de la fracción que se quiere racionalizar, que contiene raíces cúbicas. El otro factor del lado derecho lo identificamos con el factor racionalizante. Su producto es una diferencia de cubos en que podremos simplificar los radicales. Para la suma tenemos esta otra fórmula $$a^3+b^3 = (a+b)( a^2-ab +b^2)$$
Ejemplo Calcular
Solución Multiplicamos todo el numerador y todo el denominador por el factor
racionalizante, en este caso el de una diferencia con raíces cúbicas. 
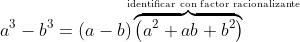
No se efectua el producto del denominador
Luego de racionalizar, se buscan los factores idénticos a cancelar, si es necesario se factoriza
Ejercicios 1) Determinar los siguientes límites \begin{array}{ll} 1.1) \ \lim_{x\rightarrow -1}\frac{ \sqrt[3]{x}+1} { x^2+x } \; \\ 1.2)\ \lim_{x\rightarrow 1}\frac{ \sqrt[3]{x}-1} { \sqrt[]{x}-1 } \\ 1.3) \ \lim_{x\rightarrow 2}\frac{ x^2-3x+2} { \sqrt[3]{x^2}-\sqrt[3]{x+2} } \; \end{array}
Solución en detalle de
cada ejercicio