Regla de l´Hôpital y formas indeterminadas
Cálculo de límites
INTRODUCCIÓN
El límiteEjemplo Encuentre
![]()
Solución Ya observamos que el límite es una forma indeterminada 0/0. Tanto la función del numerador y denominador son derivables, entonces el límite se puede determinar usando la regla de l´Hôpital
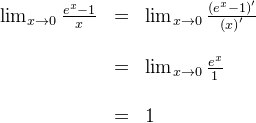
La regla se sigue cumpliendo en el caso que se tenga una forma indeterminada del tipo infinito sobre infinito. Esto es si

También se cumple para límites laterales, es decir, si c es sustituido por $c^+$ o $c^-.$
Finalmente, se cumple para límites en el infinito, c por ∞.
Ejemplo Encuentre
![]()
Solución Al intentar aplicar sustitución directa nos percatamos que tenemos una indeterminación 0/0. Efectivamente, tenemos una indeterminación pues
![]()
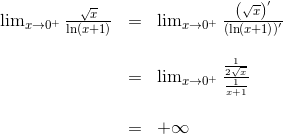
Video 1 DESPUÉS DE APLICAR L´HÔPITAL
Se esquematiza distintas situaciones que pueden ocurrir después de aplicar l'Hôpital y cómo proceder para determinar el límite resultante. Se muestran cuatro ejemplos de límites de cocientes que presentan formas indeterminadas cero sobre cero o infinito sobre infinito en que luego de aplicar l´Hôpital en alguno desaparece la indeterminación y en otros sigue, en estos casos se insiste en simplificar antes de volver aplicar l´Hôpital, logrando resolver el límite de una manera más sencilla.
Ejercicios Encontrar
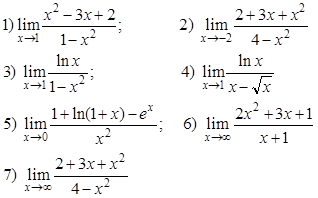
Pulsa el botón para ver las respuestas
Respuestas
1) 1/2;
2) -1/4;
3) -1/2;
4) 2;
5) -1 ;
6) ∞
7) -1;
COMENTARIOS SOBRE LA REGLA DE L´HÔPITAL
¿Siempre se puede obtener el valor del límite usando L´Hôpital?Se muestra distintos ejemplos que contesta la pregunta, haciendo comentarios a ser tomados en cuenta a la hora de usar la regla de L´Hôpital.
Ejercicios Encontrar
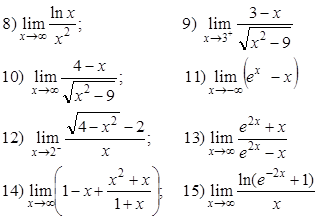
Respuestas
8) 0; 9) 0; 10) -1; 11) 0; 12) – ∞ ; 13) 1; 14) 1; 15) 2;
8) 0; 9) 0; 10) -1; 11) 0; 12) – ∞ ; 13) 1; 14) 1; 15) 2;
ENCONTRAR LÍMITES CERO POR INFINITO USANDO LA REGLA DE L'HÔPITAL
Se muestran ejemplos sencillos de límites que presentan forma indeterminada cero por infinito que pueden ser resueltos simplificando, mostrando que un límite que presenta esta forma puede valer cero, una constante o infinito, entre otras posibilidades. Sin embargo, hay límites con estas formas indeterminadas que no pueden ser resueltos simplificando, tampoco directamente usando e la regla de L´Hôpital pues no se tienen límites de cocientes, entonces se reescriben como un cociente.
Ejercicios Hallar
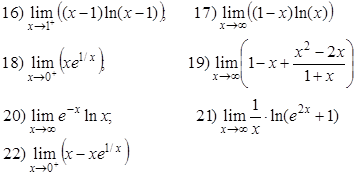
Respuestas
16) 0; 17) –∞ ; 18) ∞ 19) –2 ; 20) 0 ; 21) 2; 22) –∞ ;
16) 0; 17) –∞ ; 18) ∞ 19) –2 ; 20) 0 ; 21) 2; 22) –∞ ;
ENCONTRAR LÍMITES UNO A LA INFINITO,
CERO A LA CERO E
INFINITO A LA CERO,
USANDO LA REGLA DE L'HÔPITAL
Pasos
1) Aplicar $e^{\ln}$ al lado derecho de la expresión $y=\lim (f(x))^{g(x)}$ $$y= e^{\ln \lim (f(x))^{g(x)}}$$
2) Usar la propiedad de continuidad en los límites $$y= e^{ \lim ( \ln (f(x))^{g(x)})}$$
3) Aplicar la propiedad del logaritmo de una potencia en el lado derecho
$$y= e^{ \lim (g(x)\cdot \ln (f(x)))}$$
4) Llevar el limite del exponente a un cociente. Aparecerá una forma indeterminada. Aplicar L'Hôpital.
Ejemplo Calcular $y=\lim_{x\to 0}(1+2x)^{\frac{5}{3x}}$
Solución
Aplicar $e^{\ln}$
Ejercicios Calcular cada uno de los siguientes límites
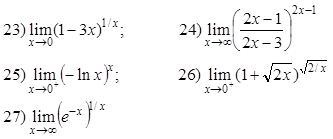
Respuestas
23) e -3; 24) e 2; 25) 1; 26) e 2;
27) No hace falta usar l'Hôpital. Al aplicar la propiedad de la potencia de una potencia y simplificar desaparece la indeterminación.
27) e -1;
23) e -3; 24) e 2; 25) 1; 26) e 2;
27) No hace falta usar l'Hôpital. Al aplicar la propiedad de la potencia de una potencia y simplificar desaparece la indeterminación.
27) e -1;
