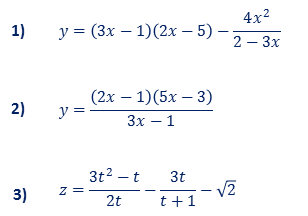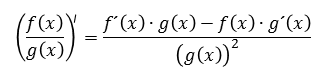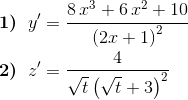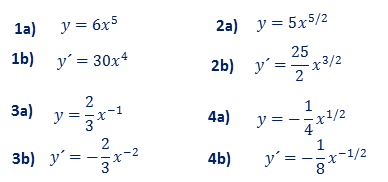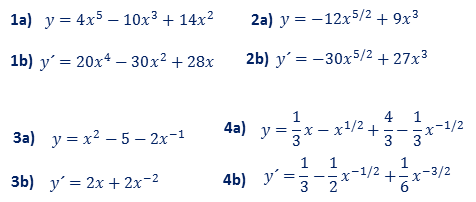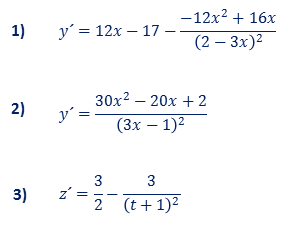Técnicas de derivación
Reglas para calcular la derivada de un producto y
un  cociente de funciones



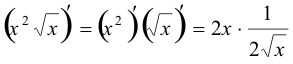
¿Es la derivada de un producto el producto de las derivadas?


X Incorrecto
La proposición es falsa Podemos reescribir la expresión: $x^2x^{1/2}=x^{5/2}$

Al derivarla obtenemos $(x^{5/2})´=\frac{5}{2}x^{3/2}\ne \sqrt{x}$
  
V correcto
La proposición es falsa Podemos reescribir la expresión: $x^2x^{1/2}=x^{5/2}$

Al derivarla obtenemos $(x^{5/2})´=\frac{5}{2}x^{3/2}\ne \sqrt{x}$



¿Es la derivada de un cociente el cociente de las derivadas?


X Incorrecto
La proposición es falsa Podemos reescribir la expresión: $\frac{x^2}{x^{1/2}}=x^{2-1/2}=x^{3/2}$

Al derivarla obtenemos $(x^{3/2})´=\frac{3}{2}x^{1/2}\ne 4x\sqrt{x}$
  
V correcto
La proposición es falsa Podemos reescribir la expresión: $\frac{x^2}{x^{1/2}}=x^{2-1/2}=x^{3/2}$

Al derivarla obtenemos $(x^{3/2})´=\frac{3}{2}x^{1/2}\ne 4x\sqrt{x}$

Contenido
1 Identificar funciones que son productos y cocientes 2 Regla del producto y cociente. Ejemplos 3 Ejemplos en que se puede reescribir para evitar aplicar estas reglas 4 Funciones más complicadas. Combinación de las reglas de la suma, producto y cociente

Has visto en las respuestas que las funciones de arriba las hemos podido derivar escribiendo la función de manera equivalente en su dominio, para luego, derivar, aplicando la regla de la potencia. Pero no siempre lo podremos o es recomendable hacerlo, como las funciones que te presentamos

     
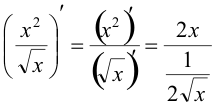
Decimos que la función h e es un producto pues puede ser interpretada como el producto de dos funciones


asi $h=fg.$

De manera similar, podemos justificar que H es un cociente de funciones.

Podemos derivar este tipo de funciones usando las reglas del producto y del cociente.




¿Cómo identificar la expresión?

Para identificar la expresión se debe tomar en cuenta la jerarquía de operaciones:
Primero potenciación y radicación.
Segundo las multiplicaciones y divisiones.
Finalmente las sumas y restas.
Las operaciones entre paréntesis tienen prioridad.

Puedes identificar si la expresión es una suma, producto o potencia viendo cual sería la última operación que harías al evaluar la expresión en un número.


Regla del producto
Sean $f$ y $g$ funciones derivables entonces

En palabras se dice que :

La derivada de un producto es
la derivada del primero por el segundo (sin derivar)
más
el primero (sin derivar) por la derivada del segundo





Regla del cociente
Sean $f$ y $g$ funciones derivables entonces



En palabras se dice que :

La derivada de un cociente es
la derivada del numerador por el denominador (sin derivar)
menos
el numerador (sin derivar) por la derivada del denominador
todo dividido
entre el cuadrado del denominador.


Notación de Leibniz y
demostraciones de las reglas


Ejemplo Encontrar la derivada de

Justificar de igualdad en igualdad la propiedad que se esta usando.
Solución Tenemos un producto, aplicamos la regla
   

Pasa el puntero sobre la imagen para ver como proceder más rápido.




Ejemplo Encontrar la derivada de

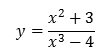
Justificar de igualdad en igualdad la propiedad que se esta usando.
Solución Tenemos un cociente, aplicamos la regla
   

Pasa el puntero sobre la imagen para ver como proceder más rápido.





Ejercicios Derivar




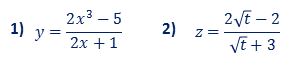
¿Se puede derivar productos y cocientes sin usar dichas reglas?

Ya se vió al comenzar esta sección cómo funciones que eran productos y cocientes fueron escritas de manera equivalente como potencias, para entonces derivarlas usando la regla de la potencia. Algunas funciones conviene escribirlas de manera equivalente antes de derivar. En la animación se dan algunas recomendaciones de reescritura antes antes de derivar.


Ejercicios
a) Escriba como un múltiplo constante por una potencia: $kx^r$
b) Derive sin usar la regla del producto y del cociente.

Solución





   

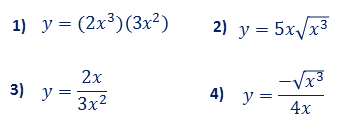
Reescribir antes de derivar

Se muestra dos situaciones en que se recomienda escribir un producto y un cociente como una suma, para derivar más rápido.
• Un monomio por una suma de potencias de la variable.
• Una fracción con denominador un monomio



Ejemplo Derive sin usar la regla del producto $$ f(x)=x^3(3x^2+2x-5)$$
Solución
Reescribir $f$ usando la propiedad distributiva
$ f(x)=x^3\cdot 3x^2+ x^3\cdot2x-x^3\cdot 5$
$ \qquad \;= 3x^5+ 2x^4-5x^3$
Derivar como una suma
$ f'(x)= (3x^5)'+ (2x^4)'-(5x^3)'$
$\qquad= 3(x^5)'+ 2(x^4)'-5(x^3)'$
$\qquad= 3\cdot 5 x^4 + 2\cdot 4 x^3-5\cdot 3 x^2$
$\qquad= 15 x^4 + 8 x^3-15 x^2$


Ejercicios
a) Escriba como una suma
b) Derive como una suma

Solución




   

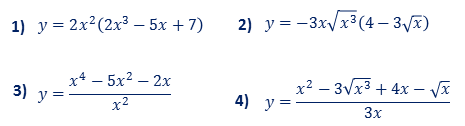
Funciones más complicadas para derivar

Suma con productos


Ejemplo
Derivar

Solución


Producto de tres funciones

Si tenemos tres funciones diferenciable, entonces se puede probar, asociando, que

Se asocian las dos primeras funciones



Ejemplo
Derivar

Solución



Derivar funciones en que se combinan sumas, productos y cocientes

Ejercicios Derivar


1) Es una diferencia. La primera regla a usar es la de la diferencia. El primer término se deriva como un producto, el segundo como un cociente.

2) Es un cociente. La primera regla a usar es la del cociente. El numerador es un producto. Se usa la regla del producto para derivarlo. No se olvide de los paréntesis.

3) Para derivarlo se usa la regla de la diferencia:
    (   )´ – (   )´ – (  )´.
Es mejor reescribir el primer término antes de derivar. Descomponiendo como una suma de fracciones con igual denominador y entonces simplificar la variable en cada término. Entonces se aplica la regla de la diferencia evitando la regla del cociente.
El segundo término se usa la regla del cociente
El tercer término es una constante, su derivada es 0.