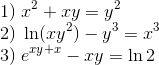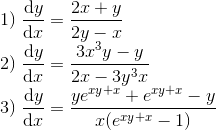Derivación implícita

Video
DERIVACIÓN IMPLÍCITA. CONCEPTOS, EL MÉTODO Y EJEMPLO

Se empieza con conceptos e ideas claves para entender el método de derivación o diferenciación implícita, pasando a establecer los pasos para obtener la derivada de una función por este método cuando la función viene dada por una ecuación en que la variable dependiente no está despejada. Un ejemplo es desarrollado usando la notación de Leibniz.

---

Resumen
La derivación implícita es una técnica que se aplica a funciones definidas implícitamente, esto es a funciones definidas por una ecuación en que la $y$ no está despejada. La ventaja de este método es que no requiere despejar $y$ para encontrar la derivada.

Para conseguir la derivada de $y$ con respecto a $ x, dy/dx: $
Primero se deriva ambos miembros de la ecuación con respecto a $x$ tomando en cuenta en todo momento que $y$ es función de $x,$ y por consiguiente al tener que derivar $y$ con respecto a $x,$ hay que aplicar la regla de la cadena.
Finalmente, se despejar $dy/dx.$

---

Video
DERIVACIÓN IMPLÍCITA. EJEMPLOS

En el video mostramos dos ejemplos de cómo obtener la derivada, $y',$ cuando la función viene determinada implícitamente por una ecuación, empleando el método de derivación o diferenciación implícita. Se usa la notación prima, $'$', se muestra cómo derivar distintos términos y se dan recomendaciones de cómo despejar $y'.$

---

Un ejemplo con logaritmo, resuelto siguiendo los pasos
A continuación, un ejemplo con logaritmos, donde es conveniente antes de derivar, reescribir la ecuación aplicando las propiedades de los logaritmos hasta que ningún logaritmo sea producto, cociente o potencia.

Ejemplo Consiga $dy/dx$ por derivación implícita

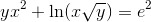
Solución
Preparamos antes de derivar, para que la derivación resulte más fácil. Como tenemos el logaritmo de un producto aplicamos la propiedad, es la suma de los logaritmos, aprovechamos de reescribir el radical


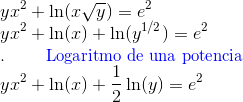
Ahora se deriva implícitamente. Se deriva el lado izquierdo y el derecho con respecto a $x.$ Recuerde que $y$ es función de $x$ El lado derecho es una constante, su derivada es cero


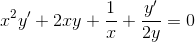Falta despejar $y'.$
Seguimos las recomendaciones para despejar una variable que está lineal en una ecuación. Primero multiplicar por el mcm de los denominadores $2xy,$ a fin de eliminarlos, queda

La última simplificación se obtuvo al sacar $-2y$ de factor común en el numerador y $x$ en el denominador. Los otros factores resultaron iguales, se cancelaron.

---

Ejercicios
Encuentre $dy/dx$ por derivación implícita.

---

---