Derivadas de las funciones logarítmicas y de
las logarítmicas compuestas, log(u(x))
Derivada del logaritmo natural
Por variados procedimientos, partiendo de distintas suposiciones, se puede demostrar que

Recuerde que ln, llamado en ocasiones logaritmo neperiano, es el logaritmo con base e. La fórmula sólo es para logaritmos naturales, enseguida, mostraremos una fórmula general para la derivada de logaritmos en cualquier base.
Derivada de logaritmo de función: $\ln(u(x))$
La regla de la cadena se puede combinar con la derivada del logaritmo natural para obtener la derivada de logaritmo compuesto con una función, ln(u(x))

$(\ln(x^2+1))'= \dfrac{1}{x^2+1}(x^2+1)'$
$\qquad= \dfrac{1}{x^2+1}(2x)$
$\qquad= \dfrac{2x}{x^2+1}$
Derivadas de logaritmos de productos, cocientes y potencias
Si tenemos un logaritmo de un producto, o de un cociente o de una potencia, conviene, antes de derivar, reescribirlo, usando las propiedades de los logaritmos, hasta que los argumentos de los logaritmos no sean productos, cocientes o potencias. En la primera animación diferenciamos de dos maneras, reescribiendo y sin reescribir. En la segunda animación mostramos dos ejemplos en que conviene sin duda reescribir el logaritmo antes de derivar.
Derivada de la función logarítmica general
Mediante la fórmula de cambio de base podemos obtener la derivada del logaritmo de $x$ con base $b$. Primero pasamos el logaritmo a base e
Reescribimos antes de derivar como el producto de un factor constante por el logaritmo natural de x
Ya podemos diferenciar, tomando en cuenta que $\ln b$ es una constante y por tanto, la fracción también lo es
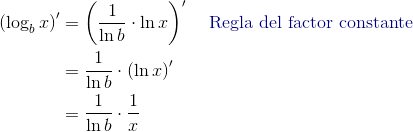
cambiamos el orden, para recordarnos que es la derivada del logaritmo natural por un factor numérico

Ejemplo $\frac{d}{dx}(\log(x))=\frac{1}{x}\frac{1}{10}$ La base es 10
Ejemplo
$\left(\left( \log_{ 3} x \right)^4 \right)' \; =
4\left( \log_ { 3}x \right)^3 (\left( \log_{ 3} x \right)'$ Regla de la potencia generalizada
$ \quad = 4\left( \log_ { 3}x \right)^3 \cdot \frac{1}{ {x} }\cdot \frac{1}{3} $
$ \quad =\frac{4\left( \log_ { 3}x \right)^3 }{3x}$
Para la derivada del logaritmo base $b$ de una función de $x$ tenemos la siguiente fórmula

Ejemplo
$\left( \log_{2 } (x^3-4x^2) \right)' \; =\dfrac{1}{x^3-4x^2}(x^3-4x^2)'\cdot \dfrac{1}{2}$
$\qquad\quad =\dfrac{1}{x^3-4x^2}(3x^2-8x)\cdot \dfrac{1}{2}$
$\qquad\quad =\dfrac{3x-8}{2(x^2-4x)}$
Se multiplico y se simplificó la fracción.
Animación
En el video se deriva dos funciones en que logaritmos se componen con raíces: el logaritmo de una raíz y la raíz de un logaritmo. En el primer caso se transforma el radical a una potencia con exponente racional y se aplica propiedades de los logaritmos antes de derivar. En el segundo ejemplo se aplica la regla de derivación de la cadena para funciones potencia y logaritmos compuestos con función.
Derivadas de funciones diversas en que aparecen logaritmos
Una metología para derivar funciones complicadas es primero analizar la función que se quiere derivar y preguntarse: es una suma, resta, producto, cociente, potencia, exponencial o logaritmo de función. Las reconocemos porque si por ejemplo es una suma, al tapar los términos no queda más nada escrito que el signo. Abajo mostramos algunos ejemplos. Pasa el puntero para ver
Ejemplos Indique si la función puede ser vista como una suma, producto, cociente, potencia, exponencial o logaritmo de función.
Pase el puntero sobre la imagen para ver la respuesta
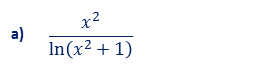

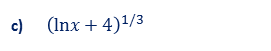

Considere reescribir para ser más fácil la derivación.
Entonces aplicar la regla. Dejar indicada la derivada y volver a hacer el mismo tipo de análisis a menos que la derivada sea inmediata.
Con esta metodología podrás derivar funciones complicadas, claro algunas derivadas son inmediatas y se podrán escribir de una vez.
Abajo está el desarrollo paso a paso de las derivadas del ejemplo.
Resolución a Resolución b Resolución c Resolución d
