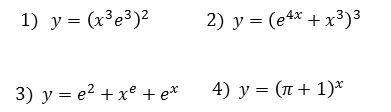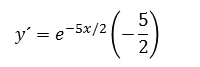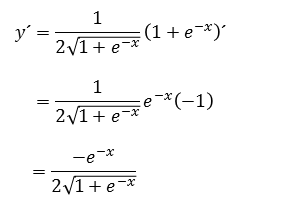Derivada de la función exponencial
Regla de la cadena para la funcion exponencial compuesta
Funciones del tipo número elevado a una función
Estamos interesados en derivar funciones en que la variable solo está en el exponente. Cuando el exponente es una función
distinta de x, hay que aplicar la regla de la cadena.
Aquí mostramos fórmulas para derivar este tipo de funciones, af(x), como y=2√x+5 y funciones en que aparecen este tipo de
expresiones, como y=x4·34x+1.
Empezamos con la derivada de la función exponencial de base $e$
Geométricamente esto se interpreta como la pendiente de la recta tangente en cualquier punto $(x,f(x))$ de la gráfica es la ordenada del punto.
Ejercicio Determine la derivada de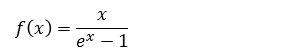
En la animación se presenta ejemplos variados en que hay que diferenciar este tipo de funciones.

Geométricamente esto se interpreta como la pendiente de la recta tangente en cualquier punto $(x,f(x))$ de la gráfica es la ordenada del punto.
Ejercicio Determine la derivada de
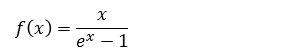
Pulsa el botón para ver las respuestas
Diferenciación de funciones exponenciales de base e compuestas con función
Son funciones que se presentan con la forma número e elevada a función. Podemos obtener la derivada aplicando la regla de la cadenaEn la animación se presenta ejemplos variados en que hay que diferenciar este tipo de funciones.
Diferenciación de funciones exponenciales de base a
Queremos derivar una función exponencial con base $a\ne 1$ distinta a e, $f(x)=a^x,\quad a>0 (\ne 1)$Podemos reescribir antes de derivar, para expresar la función en términos de la exponencial con base e. Para eso, usamos la definición del logaritmo $ a^x\quad =e^{ln(a^x)} \qquad$ aplicar la propiedad del logaritmo de una potencia
$\qquad = e^{xln(a)} $
Podemos reescribir antes de derivar, para expresar la función en términos de la exponencial con base e. Para eso, usamos la definición del logaritmo Así, obtenemos que Date cuenta que si la base no es $e$, entonces aparece el factor logaritmo neperiano de la base.
Ejemplo
![]()
Diferenciación de funciones exponenciales de base a compuesta con función
También podemos aplicar la regla de la cadena para encontrar una fórmula para exponenciales de funciones con base a, mayor que 0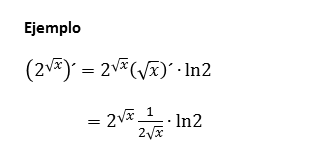
En los ejemplos de la animación podrás ver cómo encontrar la derivada de funciones que contienen la forma exponencial compuesta con base distinta a e. No te olvides multiplicar por el logaritmo natural de la base.
REESCRIBIR ANTES DE DERIVAR
Podemos usar las propiedades de los exponentes junto con otras propiedades de los números reales a fin de escribir de manera equivalente la función a derivar, para calcular la derivada de una forma más fácil.En la animación y en los ejercicios resueltos podrás ver cómo se aplican estos consejos
Ejercicio Reescribir la función y luego derivar
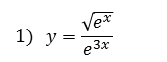
2) $\; y=\sqrt{\dfrac{e^x+1}{e^x} }$
POTENCIAS Y EXPONENTES COMBINADOS
Presentamos una animación con distintos casos en que aparecen funciones potencia y exponenciales combinados. Abajo algunos ejercicios resueltos y otros con la respuesta que permite intuir la regla aplicada.Ejercicios Derive cada una de las siguientes funciones.