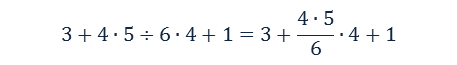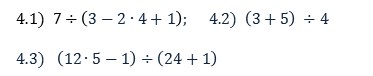PARÉNTESIS ANIDADOS, OCULTOS, SUPERFLUOS
EN OPERACIONES COMBINADAS CON NÚMEROS ENTEROS
Para romper la jerarquía de las operaciones se usan los paréntesis. A veces hace falta más de un par
de paréntesis para escribir la expresión. En otras ocasiones usamos pares de paréntesis que no hacen falta,
se llaman paréntesis superfluos. Otras veces se tienen paréntesis ocultos, que cuando se reescribe
la expresión de otra manera deben aparecer. Ejemplos ayudan explicar distintas situaciones que se pueden
presentar en Matemáticas básicas, aritmética y álgebra, así como en programación.
PARÉNTESIS ANIDADOS
DISTINTAS FORMAS DE ESCRIBIR LA EXPRESIÓN
CORCHETES Y LLAVES
A veces se necesita más de un par de paréntesis para escribir la expresión numérica, como la siguiente expresión
Hay paréntesis más internos que otros. Para visualizar la expresión, cuando hay a lo sumo tres pares de signos de agrupación se usan paréntesis, corchetes y llaves para indicar el más interno, el siguiente y el externo respectivamente. Así la expresión anterior quedaría escrita como
En muchos programas de computación colorean los paréntesis para indicar cuál cierra con cuál. Esto permite tener más de tres signos de agrupación anidados en que se distigue las contenciones. Una alternativa es usar un mismo color, oscuro para el par más interno e ir aclarando.
En la escritura manual, podemos escribir el par de paréntesis más interno más pequeño, e ir aumentando su tamaño de adentro hacia afuera.
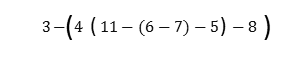
El orden de precedencia en las operaciones lo tiene las operaciones contenidas en el par de paréntesis más interno. Si hay varias operaciones dentro de este par de paréntesis, se determina su valor respetando la jerarquía de las operaciones.
Luego, en la expresión resultante se busca eliminar el par de signos de agrupación que quedó como más interno y así se sigue hasta deshacernos de todos los signos de agrupación.
Se dice que se resuelven los paréntesis de adentro hacia afuera
Ejemplo Evaluar

GRUPOS ANIDADOS DE PARÉNTESIS INDEPENDIENTES
En ocasiones se tienen varios grupos independientes de paréntesis anidados. Abajo mostramos una expresión aritmética con dos grupos de paréntesis anidados. Pasa el puntero sobre la imagen y podrás apreciar como se ha coloreado los paréntesis perteneciente a un grupo anidado de azul y los del otro grupo de rojo.
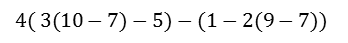
Estructuras anidadas independientes pueden ser calculadas de manera simultánea.
Ver cómo se puede determinar el valor de la expresión anterior
Ejercicios para practicar 1) Para cada paréntesis que abre indique cuál lo cierra.
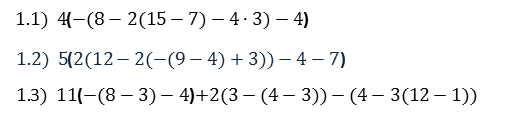
Usando paréntesis, llaves y corchetes
Usando colores
Usando tamaños
2) Determine el valor numérico de cada una de las expresiones del ejercicio anterior.
Abajo se tiene la codificación en Excel de la expresión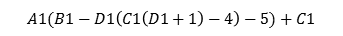
Para los valores de A1,B1,C1 y D1 –1 5, 6 y 2 respectivamente, el resultado de la evaluación es 34.
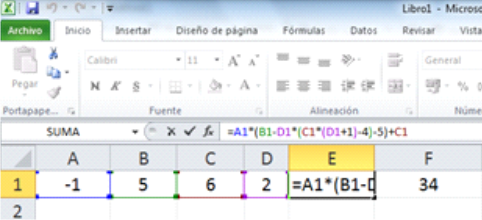
Excel colorea el paréntesis que abre con el que cierra del mismo color. También agrega colores distintivos a las variables para identificarlas rápidamente.
El usuario al codificar tiene que anotar "*" para indicar la multiplicación

En ocasiones se tienen varios grupos independientes de paréntesis anidados. Abajo mostramos una expresión aritmética con dos grupos de paréntesis anidados. Pasa el puntero sobre la imagen y podrás apreciar como se ha coloreado los paréntesis perteneciente a un grupo anidado de azul y los del otro grupo de rojo.
Estructuras anidadas independientes pueden ser calculadas de manera simultánea.
Ver cómo se puede determinar el valor de la expresión anterior
Ejercicios para practicar 1) Para cada paréntesis que abre indique cuál lo cierra.
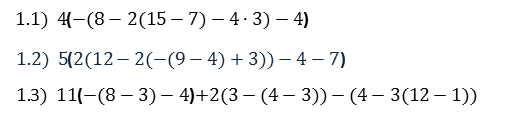
Usando paréntesis, llaves y corchetes
Usando colores
Usando tamaños
2) Determine el valor numérico de cada una de las expresiones del ejercicio anterior.
Abajo se tiene la codificación en Excel de la expresión
Para los valores de A1,B1,C1 y D1 –1 5, 6 y 2 respectivamente, el resultado de la evaluación es 34.

Excel colorea el paréntesis que abre con el que cierra del mismo color. También agrega colores distintivos a las variables para identificarlas rápidamente.
El usuario al codificar tiene que anotar "*" para indicar la multiplicación
PARÉNTESIS SUPERFLUOS O INNECESARIOS
A veces para enfatizar o entender mejor una operación aritmética se usan paréntesis que no son necesarios. Otras veces, como es el caso del programador, se utiliza paréntesis innecesarios para estar seguro del orden que se efectuarán las operaciones. Si se tiene claro el orden de precedencia de las operaciones se puede evitar sobrecargar la expresión con paréntesis.En la expresión
los paréntesis son rebundantes. Ella puede ser escrita como
La jerarquía de las operaciones, establece que las multiplicaciones tienen precedencia sobre la suma. La primera multiplicación que se hace es la aparece más a la izquierda y luego la otra. Al escribir la expresión con paréntesis nos permitir decir sin duda que la expresión es una suma.
Ejercicios 3) Elimine los paréntesis innecesarios. No realice ninguna operación. Justifique.
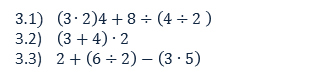
PARÉNTESIS OCULTOS O INVISIBLES
De acuerdo como se escriba algunas expresiones pueden hacer falta o no los paréntesis. Cuando en una expresión escrita de una forma no hace falta los paréntesis, pero si se reescriben de otra forma si hace falta los paréntesis hablamos de paréntesis ocultos o invisibles en la expresión que no hace falta escribirlos. Abajo expondremos algunos casos en que se presentan los paréntesis ocultosFRACCIONES CON DENOMINADOR O NUMERADOR CON MÁS DE UNA OPERACIÓN.
La fracción
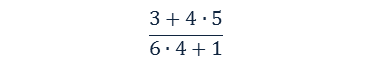
puede ser escrita como una división. Al tener tanto el numerador como denominador más de un operador hace falta paréntesis.
¿Que pasa si no escribimos paréntesis?
RADICALES CON RADICANDO CON MÁS DE UNA OPERACIÓN
La expresión
puede ser reescrita usando la notación de exponente racional. Como hay más de una operación en el radicando aparecen los paréntesis ocultos.
La base es todo el radicando de la expresión anterior
¿Cuál es la expresión con radicales si no escribimos paréntesis?
Otro ejemplo más del paréntesis invisible surge al codificar expresiones en algunas aplicaciones matemáticas y calculadoras que usan "^" para indicar la exponenciación. Si el exponente tiene más de un operador es necesario introducir el exponente entre paréntesis.
La expresión
debe ser codificada con el signo "^" como
¿Qué pasaría si no escribimos paréntesis?
Ejercicios para practicar 4) Escriba las siguientes fracciones usando el signo " ÷ " de la división
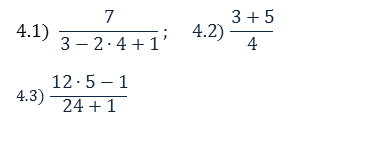
5) Escriba las siguientes expresiones suprimiendo el signo radical. No efectúe ninguna operación.
6) Codifique las siguientes expresiones. No efectúe ninguna operación.